Предмет: Математика,
автор: Aleha08
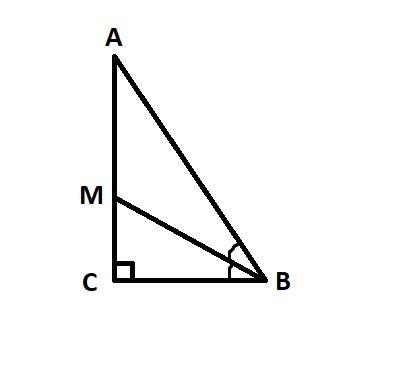
Углы треугольника АВС относятся так: \angle A:\angle B:\angle C=1:2:3. Биссектриса ВМ угла ABC равна 6. Найдите длину отрезка МС. Запишите решение и ответ, помогите пожалуйста
Ответы
Автор ответа:
18
Ответ:
Пошаговое объяснение:
прямоугольный.
BM — биссектриса ⇒
Рассмотрим ΔMCB: катет MC лежит напротив против угла в 30° ⇒
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Naurim
Предмет: Русский язык,
автор: Viki2007
Предмет: Русский язык,
автор: Суэлен
Предмет: Русский язык,
автор: Ватрушка25