Предмет: Геометрия,
автор: ncuxuka
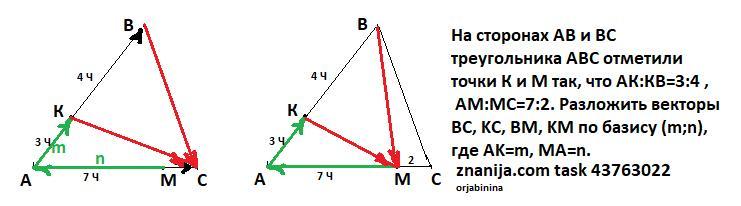
На сторонах АВ и ВС треугольника ABC отметили точки К и М так, что АК:КВ=3:4 ,
АМ:МС=7:2. Разложить векторы BC, KC, BM, KM по базису (m;n), где AK=m, MA=n.
Ответы
Автор ответа:
1
На сторонах АВ и ВС треугольника ABC отметили точки К и М так, что АК:КВ=3:4 , АМ:МС=7:2. Разложить векторы BC, KC, BM, KM по базису (m;n), где AK=m, MA=n.
Объяснение:
На сторону АВ приходится 3+4=7 частей, сторону АС- 9 частей.
1) Вектор ВС=( по правилу разности )= АС- АВ= =
.
2) Вектор КС=( по правилу разности )= АС- АК= =
.
3) Вектор ВМ=( по правилу разности )= АМ- АВ= =
.
3) Вектор КМ=( по правилу разности )= АМ- АК= =
.
Приложения:
ncuxuka:
Спасибо большое!
Похожие вопросы
Предмет: Русский язык,
автор: НевскаяИрина
Предмет: Русский язык,
автор: sinitsyna1973
Предмет: Русский язык,
автор: ТОМАТПОМИДОРОС
Предмет: Русский язык,
автор: fssaap5u4uv