Предмет: Математика,
автор: aaa03
Найти неопределенные интегралы.
Приложения:
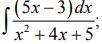
kirillshulzhik:
штото из ряда фантастики
Ответы
Автор ответа:
1
Ответ:
В числителе делаем производную знаменателя
Похожие вопросы
Предмет: Русский язык,
автор: ivanitskayaelen
Предмет: Русский язык,
автор: Foxy197
Предмет: Русский язык,
автор: deniell1500
Предмет: Литература,
автор: manzherin
Предмет: Немецкий язык,
автор: shimanskayav