Решить квадратное уравнение используя теорему виета и разложить по формуле квадратного трёхчлена
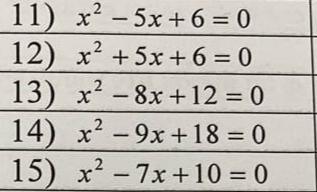
Ответы
11) x² - 5x + 6 = 0
x₁ + x₂ = 5
x₁ * x₂ = 6
x₁ = 2 x₂ = 3
x² - 5x + 6 = (x - 2)(x - 3)
12) x² + 5x + 6 = 0
x₁ + x₂ = - 5
x₁ * x₂ = 6
x₁ = - 2 x₂ = - 3
x² + 5x + 6 = (x + 2)(x + 3)
13) x² - 8x + 12 = 0
x₁ + x₂ = 8
x₁ * x₂ = 12
x₁ = 2 x₂ = 6
x² - 8x + 12 = (x - 2)(x - 6)
14) x² - 9x + 18 = 0
x₁ + x₂ = 9
x₁ * x₂ = 18
x₁ = 6 x₂ = 3
x² - 9x + 18 = (x - 6)(x - 3)
15) x² - 7x + 10 = 0
x₁ + x₂ = 7
x₁ * x₂ = 10
x₁ = 2 x₂ = 5
x² - 7x + 10 = (x - 2)(x - 5)
Ответ:
В решении.
Объяснение:
Решить квадратное уравнение используя теорему Виета и разложить по формуле квадратного трёхчлена.
Решить:
11) х² - 5х + 6 = 0
По теореме Виета:
х₁ + х₂ = 5;
х₁ * х₂ = 6;
х₁ = 3; х₂ = 2.
12) х² + 5х + 6 = 0
По теореме Виета:
х₁ + х₂ = -5;
х₁ * х₂ = 6;
х₁ = -3; х₂ = -2.
13) х² - 8х + 12 = 0
По теореме Виета:
х₁ + х₂ = 8;
х₁ * х₂ = 12;
х₁ = 4; х₂ = 2.
14) х² - 9х + 18 = 0
По теореме Виета:
х₁ + х₂ = 9;
х₁ * х₂ = 18;
х₁ = 6; х₂ = 3.
15) х² - 7х + 10 = 0
По теореме Виета:
х₁ + х₂ = 7;
х₁ * х₂ = 10;
х₁ = 5; х₂ = 2.
Разложить:
11) х² - 5х + 6;
(х² - 2*х*2,5 + 2,5²) - 2,5² + 6 =
= (х² - 2*х*2,5 + 2,5²) - 6,25 + 6 =
= (х - 2,5)² -0,25;
12) х² + 5х + 6;
(х² + 2*х*2,5 + 2,5²) - 2,5² + 6 =
= (х² + 2*х*2,5 + 2,5²) - 6,25 + 6 =
= (х + 2,5)² - 0,25;
13) х² - 8х + 12;
(х² - 2*х*4 + 4²) - 4² + 12 =
= (х² - 2*х*4 + 4²) - 16 + 12 =
= (х - 4)² - 4;
14) х² - 9х + 18;
(х² - 2*х*4,5 + 4,5²) - 4,5² + 18 =
= (х² - 2*х*4,5 + 4,5²) - 20,25 + 18 =
= (х - 4,5)² - 2,25;
15) х² - 7х + 10;
(х² - 2*х*3,5 + 3,5²) - 3,5² + 10 =
= (х² - 2*х*3,5 + 3,5²) - 12,25 + 10 =
= (х - 3,5)² - 2,25.