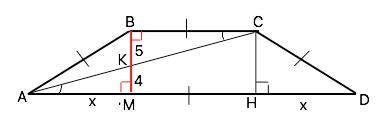
В равнобедренной трапеции ABCD, AD параллельно BC, AB=BC=CD. Высота BM пересекает диагональ AC в точке K. BK=5 , KM=4. Найдите периметр трапеции ABCD.
Ответы
Ответ: 84
Пошаговое объяснение: в приложенном файле

Ответ: 84 (ед. длины)
Пошаговое объяснение (подробно):
В трапеции АВСD стороны АВ=ВС=СD (дано).
∆ АВС - равнобедренный, а∠ВСА=∠СAD (свойство накрестлежащих углов).
ВМ - высота трапеции,⇒ ∆ АВМ – прямоугольный.
ВМ=ВК+КМ=5+4=9
Примем АМ=х.
Тогда по т.Пифагора АВ=√(х²+9²)=√(х²+81)
Треугольник КВС ~∆ КМА ( по равным углам).
Из их подобия следует ВС:АМ=ВК:КМ
(√(х²+81)):х=5:4
Возведем обе части уравнения в квадрат. ⇒
(х²+81):х=25:16 =>
16•81+16х²=25х²
16•81=х²•(25-16)
16•81=9х²
16•9=х² ⇒
х=√144=12
Из ∆ АВМ по т.Пифагора АВ=15 ( можно не высчитывать, если заметить, что это треугольник египетский с отношением сторон 3:4:5)
Т.к. ВМ и СН перпендикулярны основаниям, ВС=МН и НD=АМ=12
Р(АВСD)= 4•АВ+2•AM=4•15+2•12=84 (ед. длины)