Question

1) x2 + 5x – 24 >0;

2)(х – 5)(х – 7)(х + 3) < 0;
Помогите решить срочно пожалуйста ​

Answer 1

Ответ:

1) x ∈ (-∞; -8) U (3; +∞)

2) x ∈ (-∞; -3) U (5; 7)

Объяснение:

1) x^2 + 5x - 24>0

x^2 + 5x - 24=0

D= √(b^2 - 4ac) = √(5^2 - 4 * 1 * (-24)) = √(25 + 96) = √121 = 11

x = (-b +/- √D)/2a

x1 = -5 + 11 / 2 =3

x2 = -5-11 /2 = -8

Получается три интервала:

x<-8

-8<x<3

x>3

чередуем знаки справа налево, первый - плюс (так как нам нужно больше, то выбираем там, где плюс)

получаем x<-8 и x>3

2) (x-5)(x-7)(x+3)<0

(x-5)(x-7)(x+3)=0

x = 0 тогда, когда один из множителей равен нулю:

x=5; x=7; x=-3

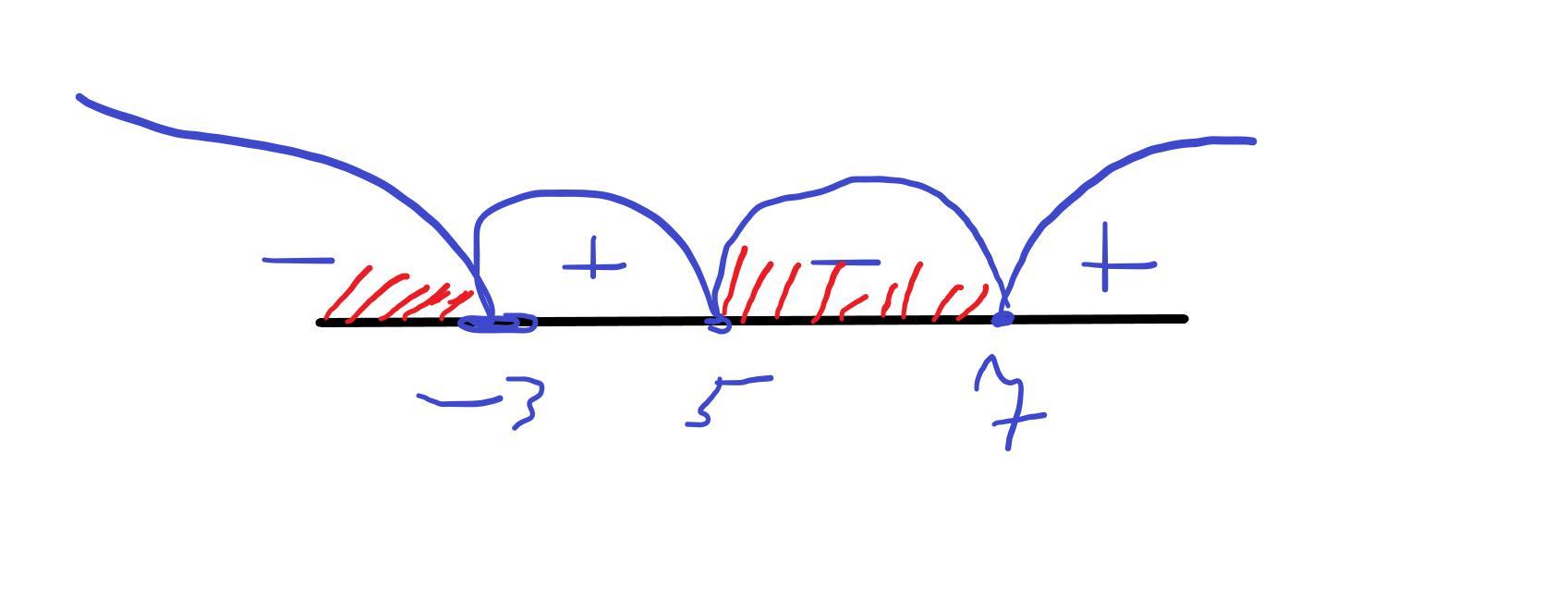
получаем четыре интервала (см фотку)

выбераем там, где минус, т. к. нужен знак < по условию

x<-3 и 5<x<7