Question

придумайте и решите задачу по чертежу
накину баллов!!!!!!!!

Answer 1

Объяснение:

угол ABC = 180 - 150 = 30 (смежные углы)

Пусть угол CAA1 = A1AB = x, тогда угол CAB = 2x.

Из треугольника ACB (ACB = 90)

2x + 30 = 90

2x = 60

x = 30

Треугольник AA1B - равнобедренный, AA1 = A1B = 20 см,

так как углы при основании AB равны.

Из тругольника ACA1 (ACA1 = 90)

CA1 = 1/2 AA1, так как CA1 - катет, что лежит напротив угла 30 градусов.

CA1 = 10 см

Из теоремы Пифагора

AC^2 = AA1^2 - CA1^2

AC^2 = (20 - 10) (20 + 10)

AC = 10 * sqrt(3) см

CB = CA1 + A1B = 10 + 20 = 30 см

Из треугольника ACB (ACB = 90) за теоремой Пифагора

AB^2 = AC^2 + CB^2

AB^2 = 300 + 900 = 1200

AB = 20 * sqrt(3) см.

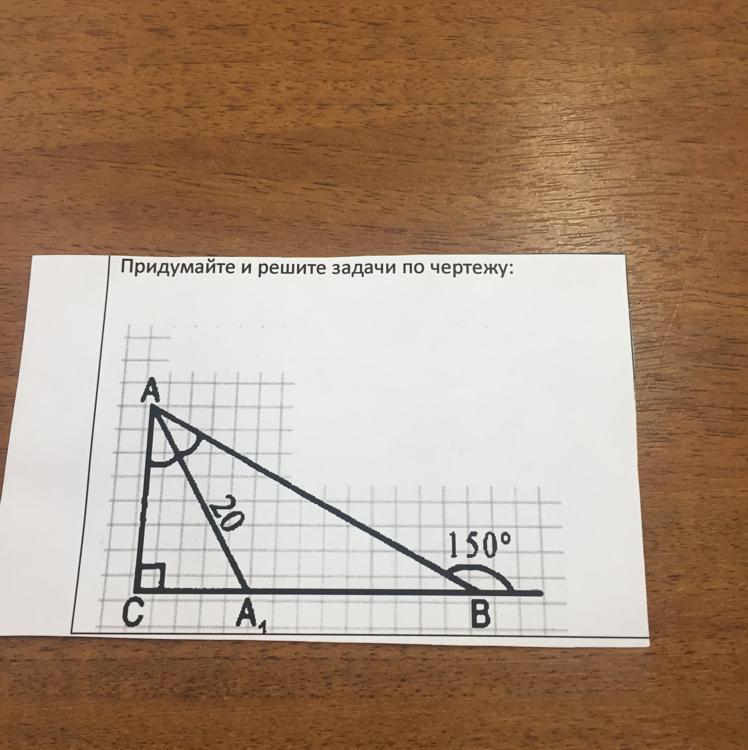
Условие:

Дан прямоугольный треугольник ACB, угол C = 90 градусов. Внешний угол при вершине B равен 150 градусов. В треугольнике проведена биссектриса AA1, AA1 = 20 см