Предмет: Алгебра,
автор: ginotopia2004
Для функции f(x) = 3x
2
-5 найдите первообразную, график которой
проходит через точку А(-1;3)
Ответы
Автор ответа:
0
Ответ:
Объяснение:
f(x) = 3x^2-5
Приложения:
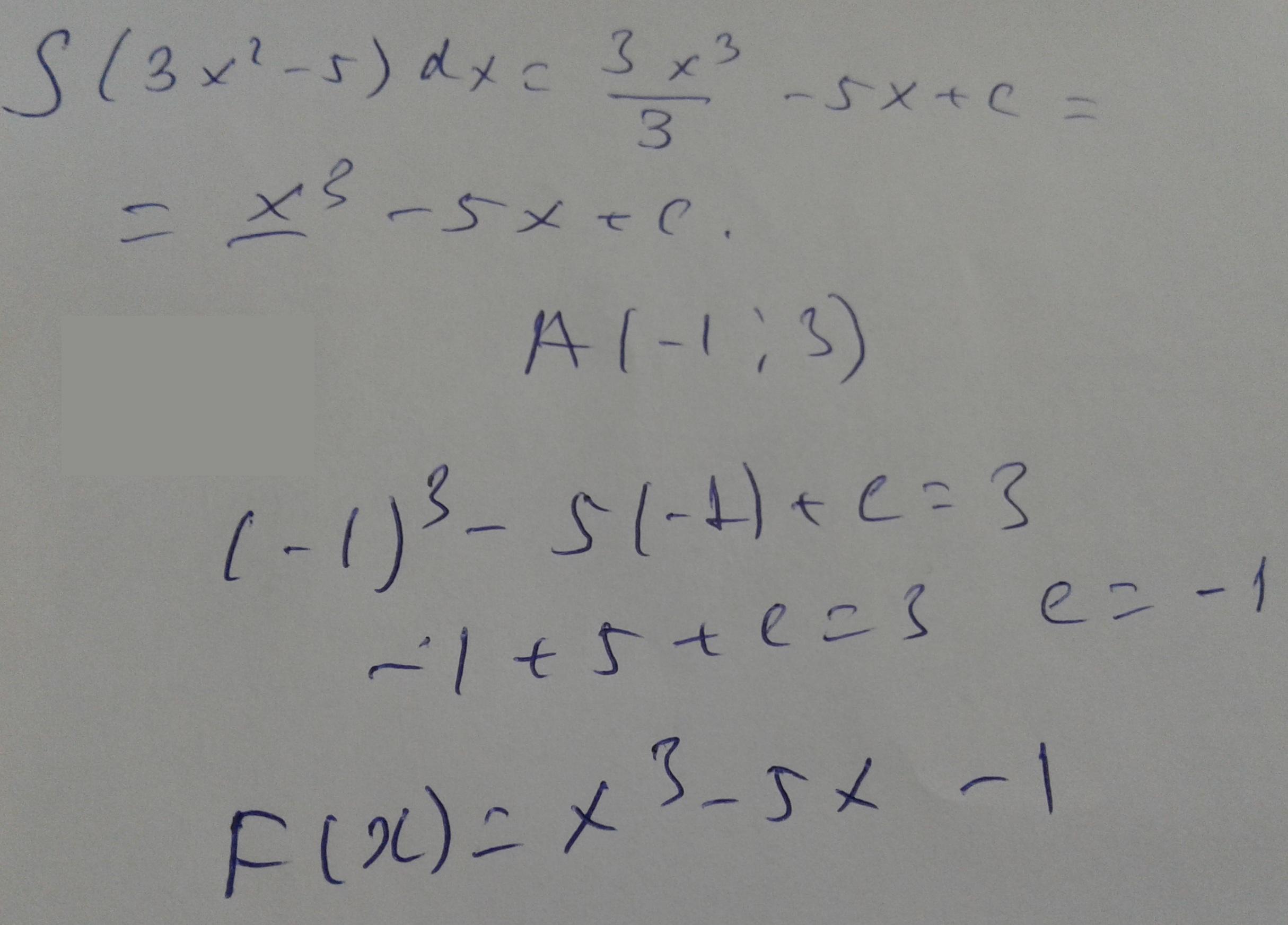
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: MarcoMuslim
Предмет: Русский язык,
автор: avagk
Предмет: Русский язык,
автор: Доска555
Предмет: Физика,
автор: акека14
Предмет: Литература,
автор: ArinaMikhailova54