Предмет: Алгебра,
автор: halandoff
Дифференциальные уравнения. Помогите решить пожалуйста! 35 баллов
Приложения:
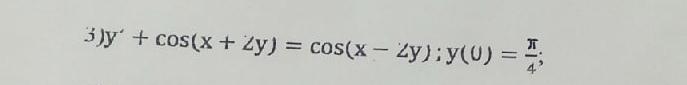
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: nickgad
Предмет: Английский язык,
автор: Znatochok
Предмет: Русский язык,
автор: АнастасияTambov
Предмет: Информатика,
автор: Stephaneremjuk01
Предмет: Математика,
автор: MiracleOne