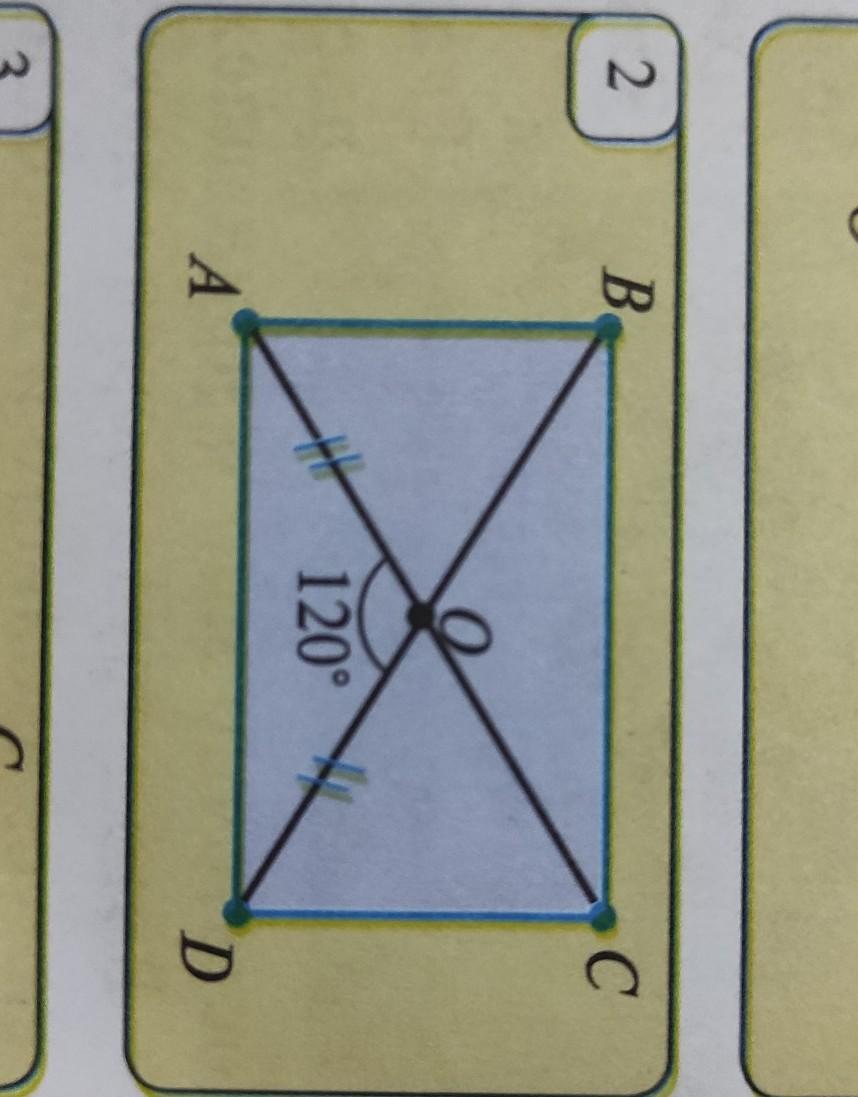
диагонали прямоугольника ABCD пересекаются в точке О рисунок 2 Найдите периметр прямоугольника если АО равно 12 см угол АОD равно 120°
Ответы
Ответ:
12+12√3 cм
Пошаговое объяснение:
Для того, чтобы найти периметр нам нужно знать длины двух сторон: P=(AB+CD)*2. Как мы знаем, угол при вершине С в треугольнике ACD равен половине угла AOD, а если не знаем, то докажем: пусть угол в 120 градусов равен фи, тогда
∠DOC=180º-∠AOD=180º-φ (как смежные).
Треугольник COD — равнобедренный с основанием CD
(OC=OD по свойству диагоналей прямоугольника). Тогда
(как угол при основании равнобедренного треугольника).
Следовательно мы доказали то, что хотели
, значит он(угол С) равен 60 градусов, тогда угол A в этом же треугольнике ACD равен 30 градусов(т.к. треугольник прямоугольный), тогда по следствию из Т. Пифагора, катет лежащий напротив угла в 30 градусов(СD) равен половине гипотенузы(AC=2AO), следовательно АО=СД, а значит этот треугольник ОСD равносторонний, что можно было понять чуть раньше, т.к. угол при вершине О = 60 градусов и угол при вершине С тоже 60, но о том, что если у треугольника углы по 60 градусов, то он равносторонний знают не все, поэтому довел до этапа с длинами. Найдем длину АD как катет по Т. Пифагора. АС=12, СД=6, следовательно АД равно
AD=√144-36=6√3
А теперь найдем периметр: 2*(6√3+6)=12+12√3 cм
Ответ:
Р = 12√3 + 24
Пошаговое объяснение:
Диагонали в точке пересечения делятся пополам =>
АС = АО +ОС = 12+ 12 = 24
BD = AC = 24
треугольник АОD равнобедренный, т. к АО =OD - по условию => угол DAO = углу ADO = 30°
Р прямоугольника = (DC + AD) * 2
найдём DC
в треугольнике ADC - п/у
DC = 1/2 AC - по св п/у треуг
DC = 1/2 24 = 12
найдём AD
проведём высоту OM и получим п/у треугольник
т. к. угол АОМ = 60° - т. к. высота в р/б треугольнике является биссектрисой => угол МАО = 30°
=> ОМ = 1/2 АО - по свойству п/у треугольника
ОМ = 1/2 12 = 6
ПО ТЕОРЕМЕ ПИФАГОРА НАЙДЁМ AD
AD² + OM² = AO²
AD² + 6² = 12²
AD² + 36 = 144
AD² = 144 - 36
AD² = 108
AD = √108 = 6√3
Р прямоугольника =( 6√3 + 12)* 2 = 12√3 + 24