Предмет: Геометрия,
автор: Аноним
ДАЮ 100 БАЛЛОВ, ПОМОГИТЕ, ПОЖАЛУЙСТА!!!
Дано:
ABC- треугольник
МР, РL, ML- средние линии
S(площадь)LMP= 60см²
tg(угла)MLP=8/15
Найти:
S(площадь)АВС
Приложения:
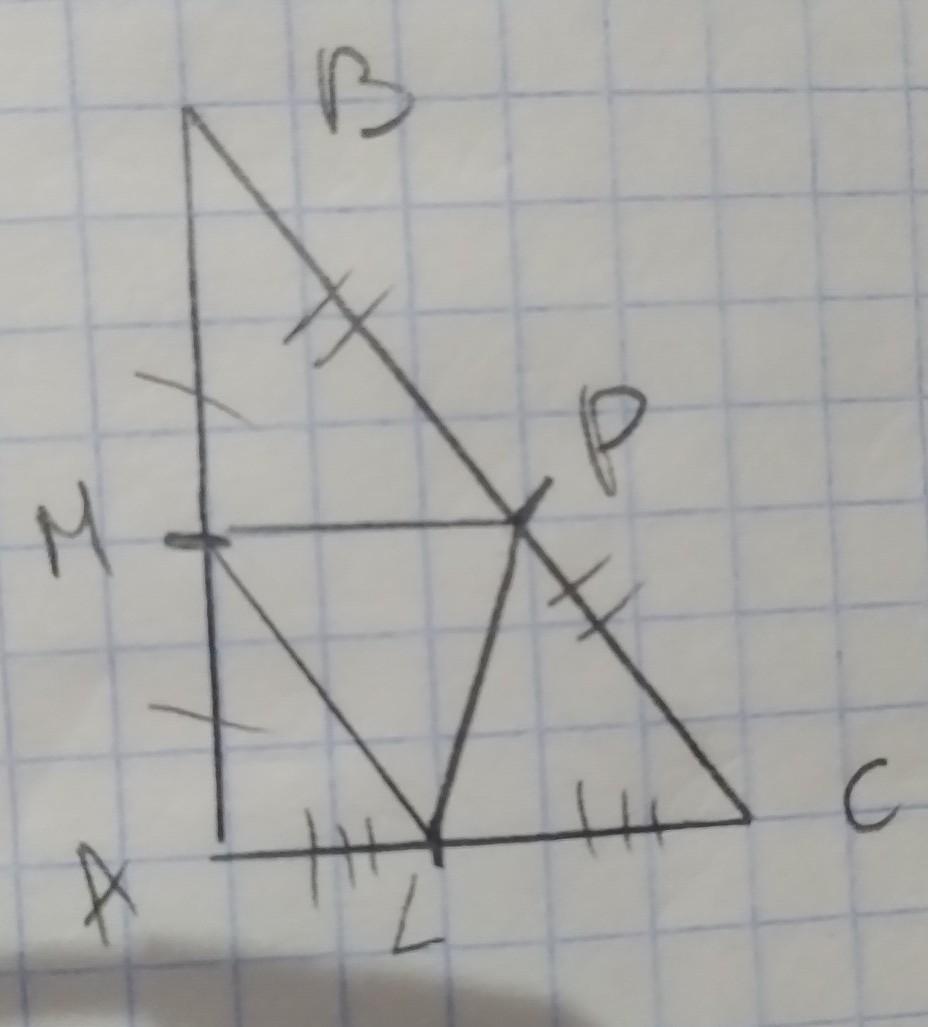
Ответы
Автор ответа:
2
Средняя линия — равна половине ей противоположного и паралельного основания.
Тоесть: (MP║AC; MP = 2*AC), (ML║BC; ML = 2*BC), (PL║AB; PL = 2*AB).
Так как треугольник — образованный средними линиями исходного треугольника — подобен исходному с коэффициентом подобия k = 1/2, то площади подобных треугольников — относятся как квадрат коэффициента подобия.
Тоесть:
Вывод: Площадь прямоугольного треугольника ABC равна: 240см².
Аноним:
Спасибо, учту! :)
Ну, что ж, удобно или нет — для кого как!
Похожие вопросы
Предмет: Русский язык,
автор: offcom2581
Предмет: Русский язык,
автор: карин7
Предмет: Українська мова,
автор: Альчик12
Предмет: ОБЖ,
автор: MiamiKing