Найдите область сходимости ряда.
Буду всем сердцем благодарна тому, кто сможет это решить!)
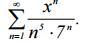
Ответы
Ответ:
Пошаговое объяснение:
это степенной ряд. запишем его в общем виде
областью сходимости степенного ряда является интервал (-R;R), где R - радиус сходимости и равен
посчитаем этот предел
таким образом, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-7;7)
теперь посмотрим сходимость ряда на концах этого интервала.
пусть х = -7, тогда мы получим ряд , это числовой знакочередующийся ряд
надо исследовать его на сходимость. исследуем по признаку Лейбница
а) по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего
- выполняется
б) по второму признаку Лейбница предел ряда по модулю должен стремится к 0
выполняется
т.е. ряд сходится x = -7 - точка сходимости
теперь пусть х = 7
тогда всё просто, как в первом случае, только ряд не знакочередующийся. он сходится x = 7 - точка сходимости
и вот получаем,
данный степенной ряд является сходящимся на интервале [-7;7]