Напишите с Дано и решение + Чертеж (номер2)

Ответы
Объяснение:
№1
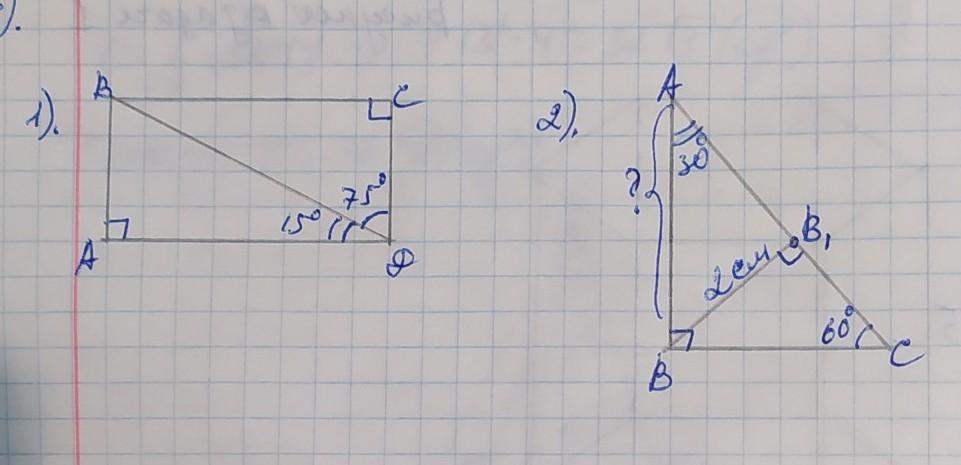
Дано: ∠ВАД=∠ВСД=90, ∠АДВ=15°, ∠ВДС=75°
ДОКАЗАТЬ: ВС || АД
======================================
ДОКАЗАТЕЛЬСТВО:
∠АДС=∠АДВ+∠ВДС=15+75=90, поэтому
∠ВАД=∠ВСД=∠АДС=90°
АВСД - четырёхугольник, а в 4-х угольнике сумма углов составляет 360° => => ∠АВС=360–3×90=360–270=90°
Тогда все углы четырёхугольника равны и каждый составляет 90°=> АВСД- прямоугольник, а у прямоугольника все противоположные стороны равны и параллельны, поэтому ВС || АД
ДОКАЗАНО
===============
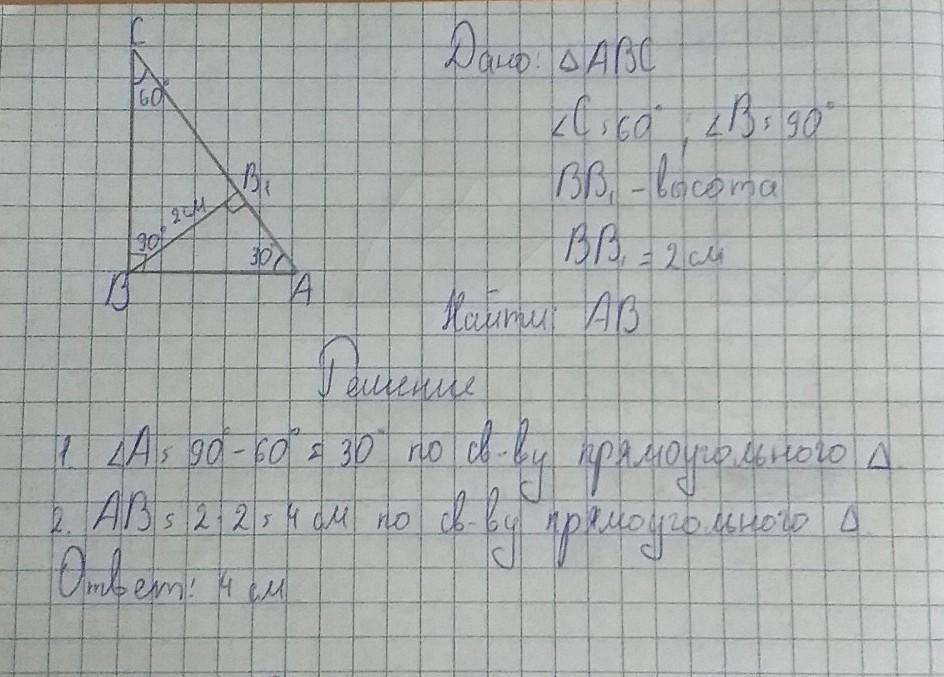
№2
ДАНО: ∆АВС, ∠В=90°, ∠С=60°, ВВ1=2см
НАЙТИ: АВ
==========================================
РЕШЕНИЕ: высота ВВ1 делит ∆АВС на 2 прямоугольных треугольника: АВВ1 и ВСВ1.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому ∠А=90–∠С=90–60=30°
∠А=30°
Рассмотрим ∆АВВ1. Он прямоугольный: ∠АВ1В=90°, АВ1, ВВ1 - катеты, АВ - гипотенуза, уголА=30°.
Катет ВВ1, лежащий напротив ∠А=30° равен половине гипотенузы, поэтому АВ=ВВ1×2=2×2=4см
АВ=4см
ОТВЕТ: АВ=4см
Объяснение:
пишу чтобы можно было отправить