Предмет: Геометрия,
автор: adamsal
Решите пожалуйста!!!!
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
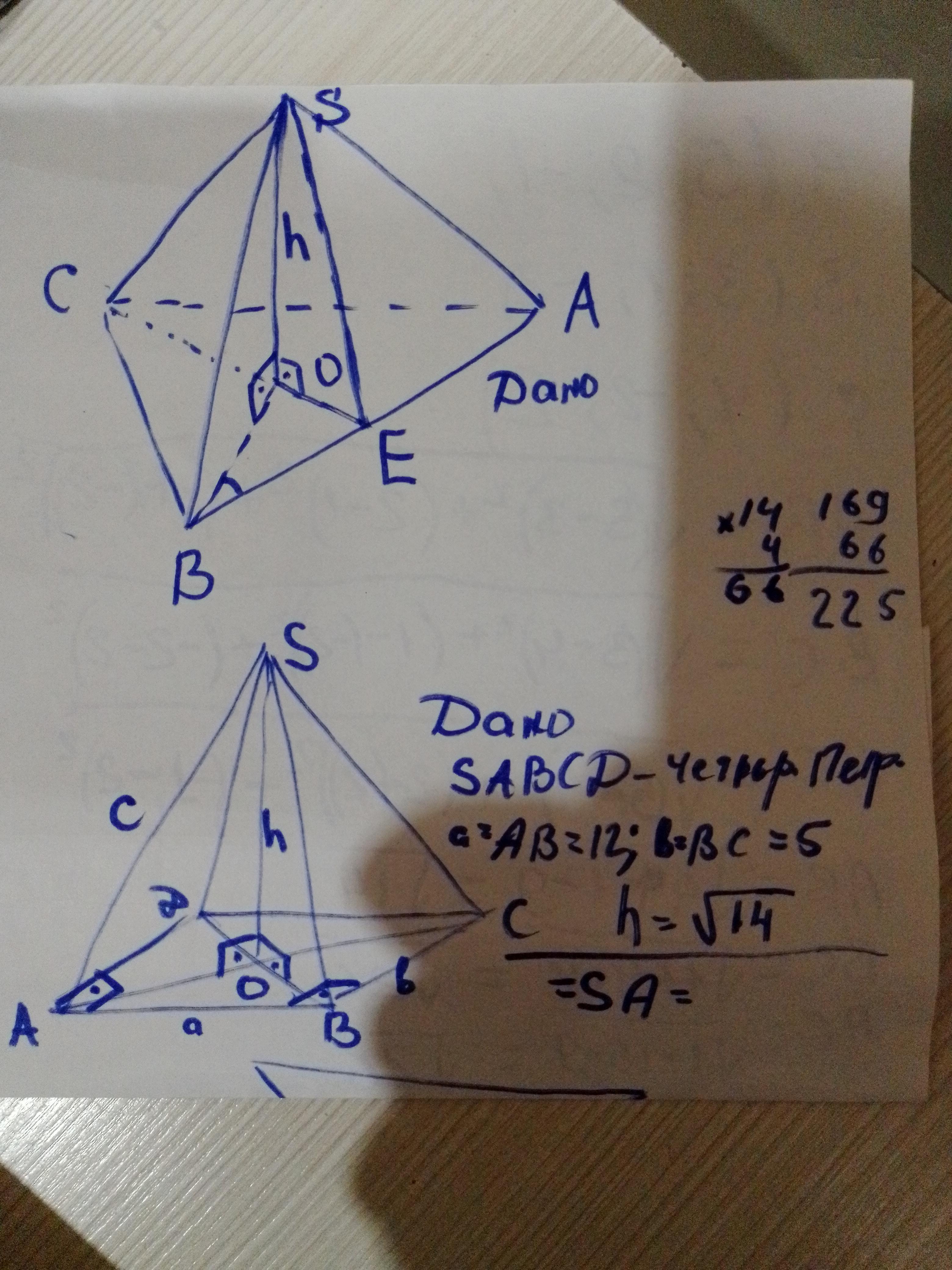
1). Дано: SABC- прав∆пирамида
АВ=a,. SO=h
Sбок=?
Решение:. .
Sбок= сумме площадей равновеликих боковых граней,
∆АВС - равносторонний => <ОСЕ=30
=>. ОВ=2ОЕ. ВЕ=а/2
По т Пифагора ∆ОЕВ находим. ОЕ
ОВ^2=(2ОЕ) ^2=(а/2)^2+ОЕ^2
ОЕ=а/(2√3)
По т Пифагора из ∆SOE находим
SE^2= h^2+(a/2√3)^2
Sбок = 3* S∆SAB
S∆SAB= 1/2a* SE
ОЕ= 18/(2√3)=3√3. ОЕ^2= 27
SE= (√22)^2+(√27)^2= √49=7
Sбок= 3*1/2*18*7= посчитаешь
2)АВСД- прямоугольник
По т Пифагора из ∆АВС определяем диагонали АС, затем из ∆ SOB по теореме Пифагора определяем ребро пирамиды.
АС = √(5^2+12^2)=√25+144)=√169=13
АО=1/2 АС =13/2
SB= √13/2)^2+(√14)^2=√169/4+14
SA=SB=SC=SD=√(225/4)=15/2
Ставим лайки!!!
Приложения:
adamsal:
Спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: kcenia2010
Предмет: Немецкий язык,
автор: Gulyuka
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: artur0206
Предмет: Математика,
автор: dimasik040440