Предмет: Математика,
автор: justfoodez
Интегралы хелп
2) винести мінус зі знаменника, виділити в знаменнику квадрат, зробити заміну;
Приложения:
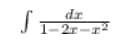
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: mehrobi93
Предмет: Русский язык,
автор: alinamatlaeva
Предмет: Русский язык,
автор: сон21
Предмет: Алгебра,
автор: reyarina
Предмет: Математика,
автор: ayooo