Question

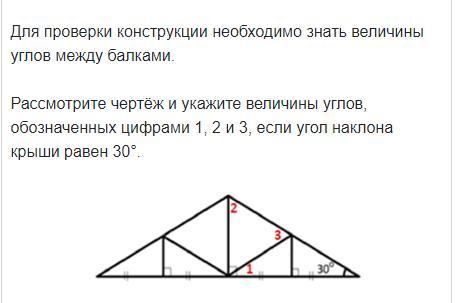
Помогите геометрия задание на углы

Answer 1

Ответ:

∠1 = 30°

∠2 = 60°

∠3 = 60°

Объяснение:

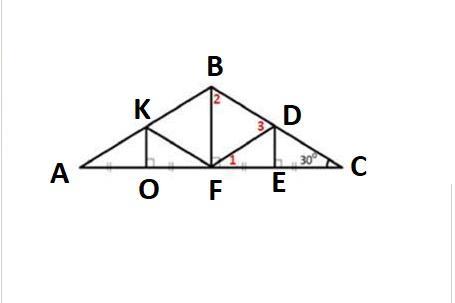
На рисунке вершины треугольников обозначены буквами!

Треугольник ΔCED = ΔDEF по двум катетам так как DE - общая и DE ⊥ FC, FE = EC по условию, следовательно соответствующие элементы треугольников равны, тогда ∠DCE = ∠DFE = ∠1 = 30°.

Рассмотрим треугольник ΔBFC. Так как по условию BF ⊥ AC, то угол ∠BFC = 90°. По теореме про сумму углов треугольника:

∠BFC + ∠FCB + ∠FBC = 180° ⇒ ∠FBC = 180° - ∠BFC - ∠FCB =

= 180° - 90° - 30°= 60°, так как угол ∠2 = ∠FBC, то угол ∠2 = 60°.

∠DFC + ∠DFB = ∠BFC ⇒ ∠DFB = ∠BFC - ∠DFC = 90° - 30° =  =60°.Рассмотрим треугольник ΔBFD. По теореме про сумму углов треугольника: ∠FBD + ∠DFB + ∠FDB = 180° ⇒ ∠FDB =

= 180° -  ∠FBD - ∠DFB = 180° - 60° - 60° = 180° - 120° = 60°. Так как угол

∠3 = ∠FDB, то угол ∠3 = 60°