Предмет: Математика,
автор: 6pnrkhrs5d
Помогите с заданиями их не так много
Первые 3 метод подстановки
Приложения:
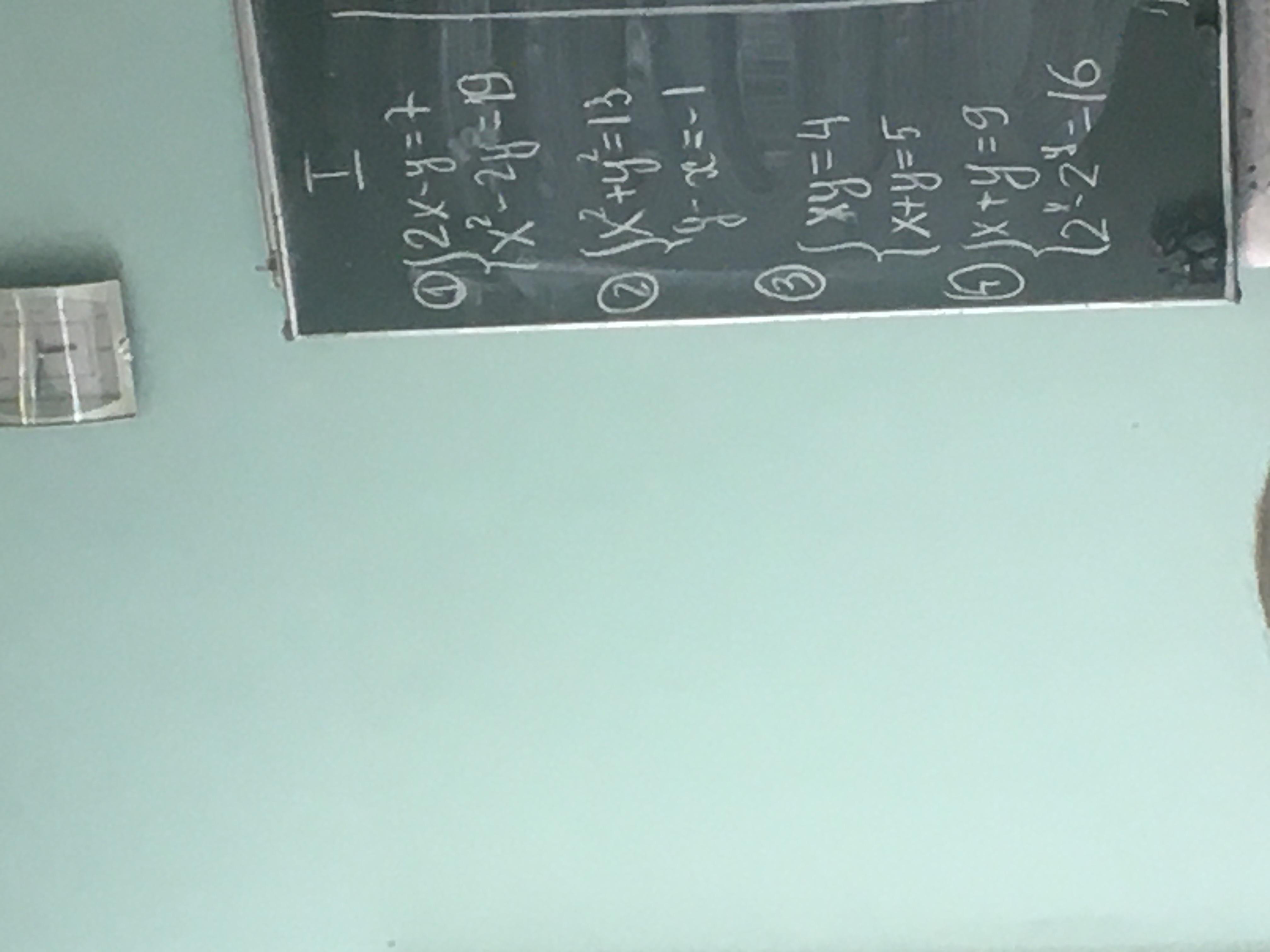
Ответы
Автор ответа:
1
1.
2.
3.
4.
Похожие вопросы
Предмет: Русский язык,
автор: ГлебВ
Предмет: Английский язык,
автор: elena260267
Предмет: Русский язык,
автор: vitalinachaukina
Предмет: Английский язык,
автор: Egorov771
Предмет: Русский язык,
автор: Love555me