Предмет: Алгебра,
автор: sans1922
розв'яжіть рівняння 2x²-4x+√5-1=0
Приложения:
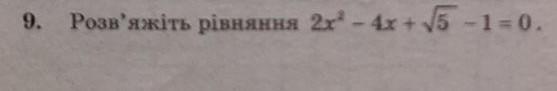
Ответы
Автор ответа:
0
Ответ:
Объяснение:
2x²-4x+√5-1=0
D=(-4)²-4·2·(√5-1)=16-8√5+8=24-8√5=(2-2√5)²; √D=√(2-2√5)²=|2-2√5|=2√5-2;
x1=4-(2√5-2)=4-2√5+2=6-2√5;
x2=4+(2√5-2)=4+2√5-2=2+2√5;
Автор ответа:
0
розв'яжіть рівняння 2x²-4x+√5-1=0
уравнения вида
найдем дискриминант
найдем корни по формуле
О т в е т:
Похожие вопросы
Предмет: Русский язык,
автор: vladikavkaz2050
Предмет: Русский язык,
автор: kurlikk1
Предмет: Русский язык,
автор: khrusheval
Предмет: География,
автор: Danik1w
Предмет: Математика,
автор: glebkirilyuk20p5sds0