Question

Точка удалена от каждой из сторон правильного треугольника на 10 см, а от плоскости треугольника — на 8 см. Найдите площадь данного треугольника. С рисунком пожалуйста​

Answer 1

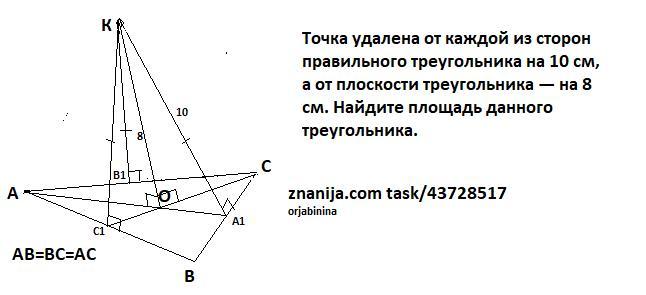
Точка удалена от каждой из сторон правильного треугольника на 10 см, а от плоскости треугольника — на 8 см. Найдите площадь данного треугольника.

Объяснение:

1) Пусть КО⊥(АВС) и КС1⊥АВ, КА1⊥ВС, КВ1⊥АС, тогда ΔКОС1=ΔКОА1=ΔКОВ1 как прямоугольные по катету( КО-общий ) и гипотенузе (КА1=КВ1=КС1=10 ) ⇒ОА1=ОВ1=ОС1 ⇒ О-центр вписанной окружности , который лежит в точке пересечения биссектрис и ОА1=ОВ1=ОС1 =r . Для равностороннего треугольника биссектриса совпадает с  высотой .

2) ΔКОА1  прямоугольный, по т Пифагора  OA1=r=√(10²-8²)=6 (cм).

3) ΔABC -равносторонний ,  a₃ =2r√3  , a₃ =12√3 см.

S(равн.треуг.)=( а²√3)/4   , S(равн.треуг.)=( (12√3)²√3)/4 =108√3 (см²)