Предмет: Алгебра,
автор: danilarutyunov37
Решите уравнения (б, г):
Приложения:
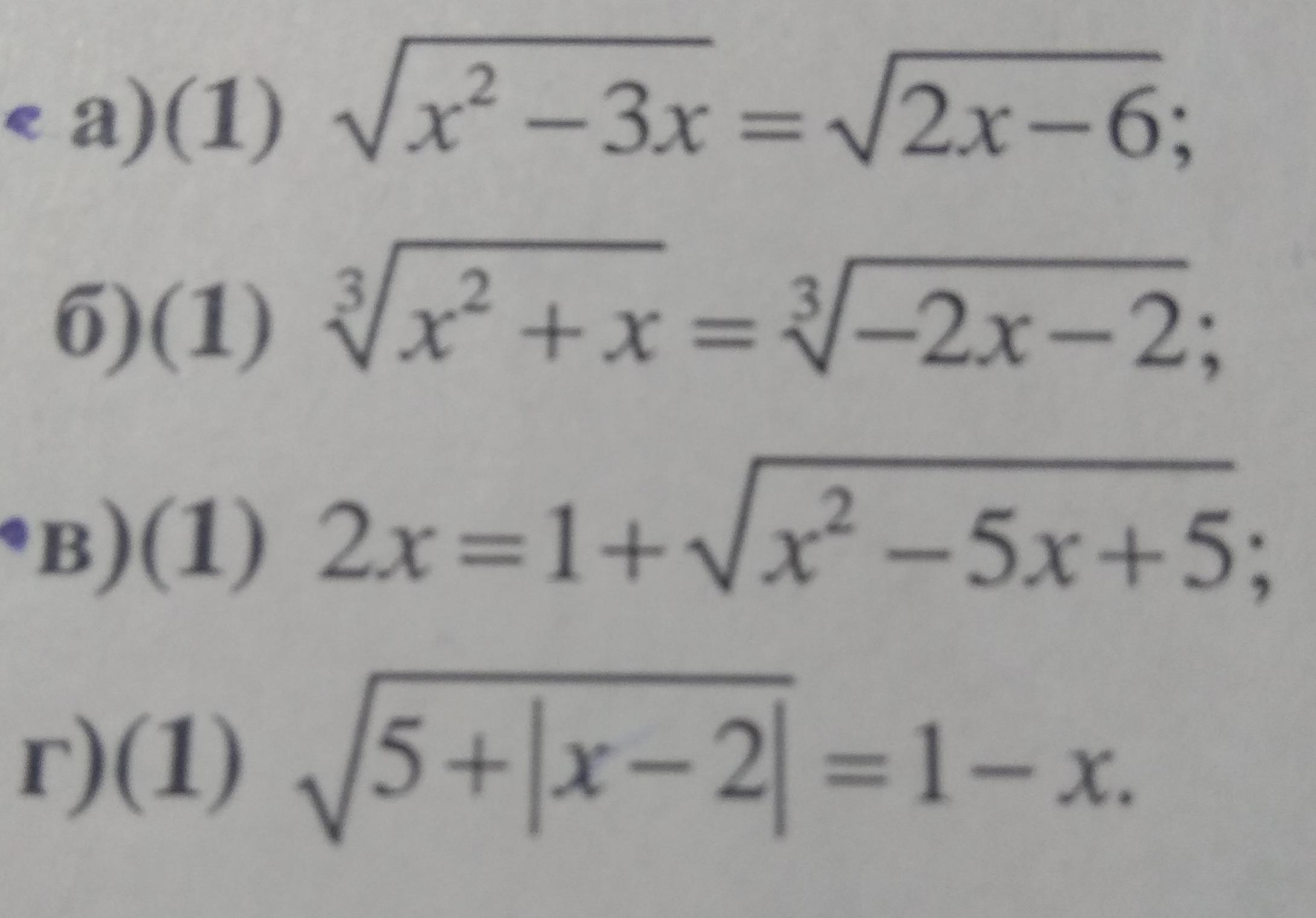
XXXGNXXX:
Слишком сложно для 5 баллов)
Ок, сейчас перевыложу.
Так сойдет?
Ответы
Автор ответа:
1
Ответ:
б) x1 = -2 ; x2 = -1
г) x = -2
Объяснение:
б)
1) Возводим обе части уравнения в степень 3 ;
2) Приводим подобные ;
3) И решаем квадратное уравнение (в данном случае через Виету).
г)
Находим пересечения и оставляем только подходящие x-ы :
x1 = -2
x2 =
Теперь проверяем их в изначальном уравнении :
Значит -2 является решением.
Значит не является решением.
Похожие вопросы
Предмет: Другие предметы,
автор: vova123450987
Предмет: Другие предметы,
автор: belyaevaka
Предмет: Русский язык,
автор: гузя4
Предмет: Математика,
автор: alsumustaeva20