Question

Медиана,  проведённая  к  гипотенузе  прямоугольного  треугольника,  равна 10  и делит прямой угол в отношении 1: 2. Найдите длину меньшего из катетов. 

Answer 1

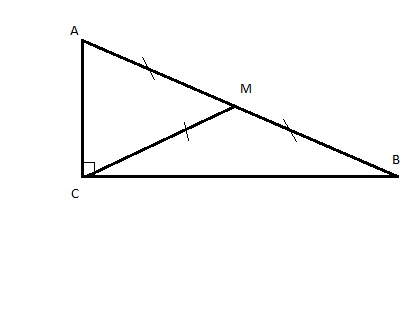
Так как прямой угол опирается на диаметр, гипотенуза прямоугольного треугольника является диаметром окружности, описанной около треугольника. Медиана, проведенная из вершины прямого угла - радиус описанной окружности, а т.М - центр окружности. Значит СМ=АМ=10=R
Известно, что медиана делит прямой угол  в соотношении 1:2, значит:
х+2х=90
3х=90
х=30
2х=60
Меньшему катету соответствует больший угол, значит 
ΔАМС - равнобедренный (АМ=СМ) и угол АСМ= 60 градусов => угол САМ=60 градусов  =>  угол СМА=60 градусов, значит  ΔАМС - равносторонний.
Меньший катет АС=10. 

Answer 2

пусть дан треугольник АВС, угол С - прямой, CR - медиана.
пусть коэффициент отношения - х, тогда х+2х=90 градусов, 3х=90, х=30 градусов. 90-30=60 градусов. Прямой угол разделился медианой на углы в 30 и 60 градусов. Медиана, проведённая из прямого угла, = половине гипотенузы, поэтому
 СК=АК= КВ=10. Треугольник АКС - равнобедренный с углом 60 градусов, значит, он равносторонний и АС=10, угол СКВ= 180-60=120 градусов т. к. углы СКВ и СМА - смежные. Катет ВС лежит против угла в 120 градусов, следовательно, он больше катета АС, т. к. против большего угла лежит большая сторона. Ответ 10