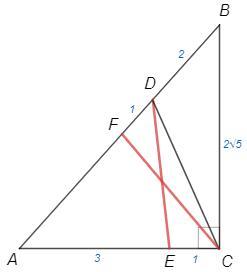
1) На стороне AB и АС прямоугольного треугольника АВС (<С = 90⁰) взято точки D и E соответственно. Найдите длину отрезка DE, если АС = 4 см, ВС = 2√5 см, СЕ = 1 см, ВD = 2 см.
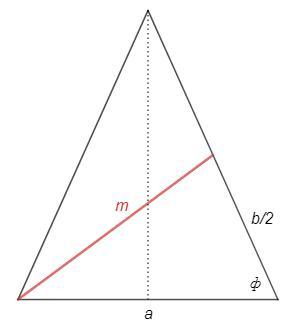
2) Основание равнобедренного треугольника равна а, а угол при основании - α. Найдите медиану треугольника, проведенной к его боковой стороны.
Ответы
1) По т. Пифагора находим АВ:
АВ² = 4² + (2√5)² = 16 + 20 = 36
АВ = 6
cos A = AC/AB = 4/6 = 2/3
AD = AB - BD = 6 - 2 = 4
AE = AC - EC = 4 - 1 = 3
В треугольнике ADE находим DE по теореме косинусов:
DE² = AD² + AE² - 2AD*AE*cos A = 16 + 9 - 2*4*3*2/3 = 9; DE = 3
2) Пусть в треугольнике АВС:
ВС = а, тогда АВ = АС = а / (2cos α), а значит ВМ = а / (4cos α)
Пусть СМ - медиана, тогда найдем её по теореме косинусов из треугольника ВСМ:
СМ² = МВ² + ВС² - 2МВ*ВС*cos α
CM² = а² / (16соs²α) + a² - a²
CM = a / (4cos)
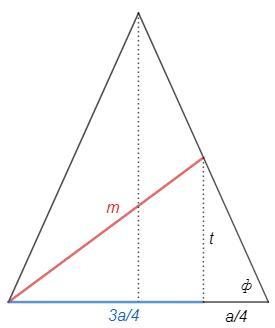
2)
t =a/4 *tgф
т. Пифагора
m^2 =(3a/4)^2 +t^2 = (a/4)^2 (9 +tgф^2)
m =a/4 *√(9 +tgф^2)
Или
b =a/2cosф => b/2 =a/4cosф
т. косинусов
m^2 =a^2 +(b/2)^2 -2a *b/2 *cosф =
= a^2 +a^2/16cosф^2 -a^2/2 =
= a^2/2 *(1 +1/8cosф^2)
m =a/2 *√(2 +1/4cosф^2)
1)
AB =√(16+20) =6 (т Пифагора)
AD =6-2 =4
AC=AD, △DAC - равнобедренный
Пусть DF=CE=1, тогда DE=CF
BF=2+1=3, CF - медиана из прямого угла, равна половине гипотенузы
DE=CF =AB/2 =3 (см)