Question

Набор данных состоит из нечётного количества пар натуральных чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы чётность суммы выбранных чисел совпадала с чётностью большинства выбранных чисел и при этом сумма выбранных чисел была как можно меньше. Определите минимальную сумму, которую можно получить при таком выборе. Гарантируется, что удовлетворяющий условиям выбор возможен.

на решу егэ на это задание есть очень длинное решение с 60+ строками. можете, пожалуйста, помочь и написать максимально сжатое решение задания на питоне?

Answer 1

Спасибо большое за интересную задачку! Получилось 32 строчки с учётом сервисных выводов и комментариями. Спрашивайте, пожалуйста, если что-то непонятно.

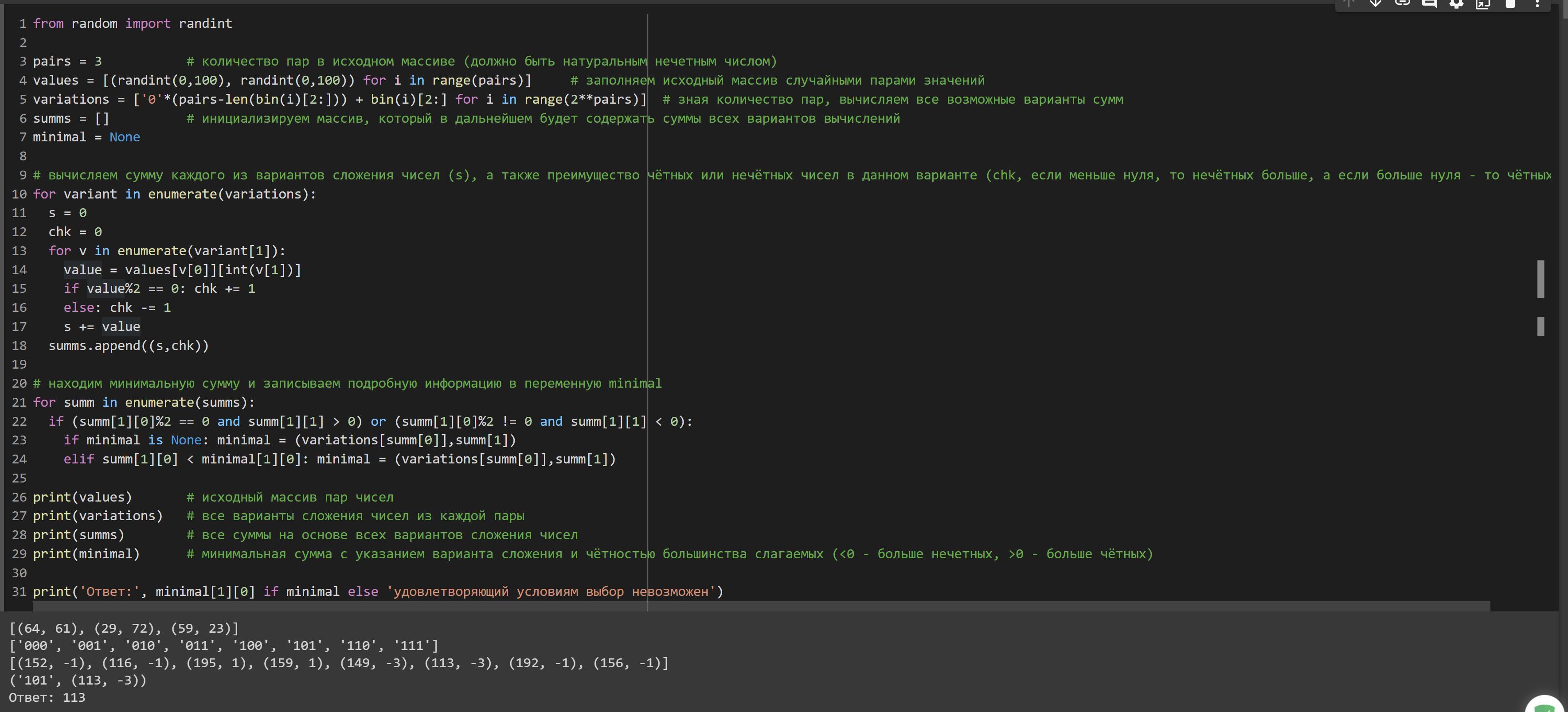
from random import randint

# инициализация переменных

pairs = 3           # количество пар в исходном массиве (должно быть натуральным нечетным числом)

values = [(randint(0,100), randint(0,100)) for i in range(pairs)]     # заполняем исходный массив случайными парами значений

variations = ['0'*(pairs-len(bin(i)[2:])) + bin(i)[2:] for i in range(2**pairs)]  # зная количество пар, вычисляем все возможные варианты сумм

summs = []          # инициализируем массив, который в дальнейшем будет содержать суммы всех вариантов вычислений

minimal = None

# вычисляем сумму каждого из вариантов сложения чисел (s), а также преимущество чётных или нечётных чисел в данном варианте (chk, если меньше нуля, то нечётных больше, а если больше нуля - то чётных)

for variant in enumerate(variations):

 s = 0

 chk = 0

 for v in enumerate(variant[1]):

   value = values[v[0]][int(v[1])]

   if value%2 == 0: chk += 1

   else: chk -= 1

   s += value

 summs.append((s,chk))

# находим минимальную сумму и записываем подробную информацию в переменную minimal

for summ in enumerate(summs):

 if (summ[1][0]%2 == 0 and summ[1][1] > 0) or (summ[1][0]%2 != 0 and summ[1][1] < 0):

   if minimal is None: minimal = (variations[summ[0]],summ[1])

   elif summ[1][0] < minimal[1][0]: minimal = (variations[summ[0]],summ[1])

print(values)       # исходный массив пар чисел

print(variations)   # все варианты сложения чисел из каждой пары

print(summs)        # все суммы на основе всех вариантов сложения чисел

print(minimal)      # минимальная сумма с указанием варианта сложения и чётностью большинства слагаемых (<0 - больше нечетных, >0 - больше чётных)

print('Ответ:', minimal[1][0] if minimal else 'удовлетворяющий условиям выбор невозможен')

После удаления комментариев и сервисных выводов получаем 20 строк кода:

from random import randint

pairs = 3

values = [(randint(0,100), randint(0,100)) for i in range(pairs)]

variations = ['0'*(pairs-len(bin(i)[2:])) + bin(i)[2:] for i in range(2**pairs)]

summs = []

minimal = None

for variant in enumerate(variations):

 s = 0

 chk = 0

 for v in enumerate(variant[1]):

   value = values[v[0]][int(v[1])]

   if value%2 == 0: chk += 1

   else: chk -= 1

   s += value

 summs.append((s,chk))

for summ in enumerate(summs):

 if (summ[1][0]%2 == 0 and summ[1][1] > 0) or (summ[1][0]%2 != 0 and summ[1][1] < 0):

   if minimal is None: minimal = (variations[summ[0]],summ[1])

   elif summ[1][0] < minimal[1][0]: minimal = (variations[summ[0]],summ[1])

print('Ответ:', minimal[1][0] if minimal else 'удовлетворяющий условиям выбор невозможен')