Предмет: Математика,
автор: ElyaMonti
срочно!
помогите доказать равенство
Приложения:
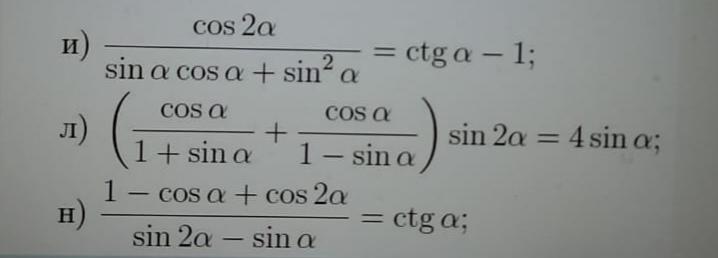
Ответы
Автор ответа:
1
Ответ:
и
л
н
Похожие вопросы
Предмет: Русский язык,
автор: keropyan4ik
Предмет: Українська мова,
автор: denpletniov
Предмет: Русский язык,
автор: санечка9
Предмет: Английский язык,
автор: СтарыйМатематик
Предмет: Алгебра,
автор: алина4045