Предмет: Алгебра,
автор: gladkih65
ДАМ МНОГО БАЛЛОВ
АЛГЕБРА 9 КЛАСС
Приложения:

Ответы
Автор ответа:
1
1. AB = {Bx - Ax; By - Ay} = {6 - 1; -7 - 5} = {5; -12}
Ответ: AB = {5; -12}
2. a · b = ax · bx + ay · by = 5 · 4 + (-2) · 3 = 20 - 6 = 14
3.
1) м = (4;-2) + (1;5) = (5;3)
2) м = 3(4;-2) - 4(1;5) = (12;-6) - (4;20) = (8;-26)
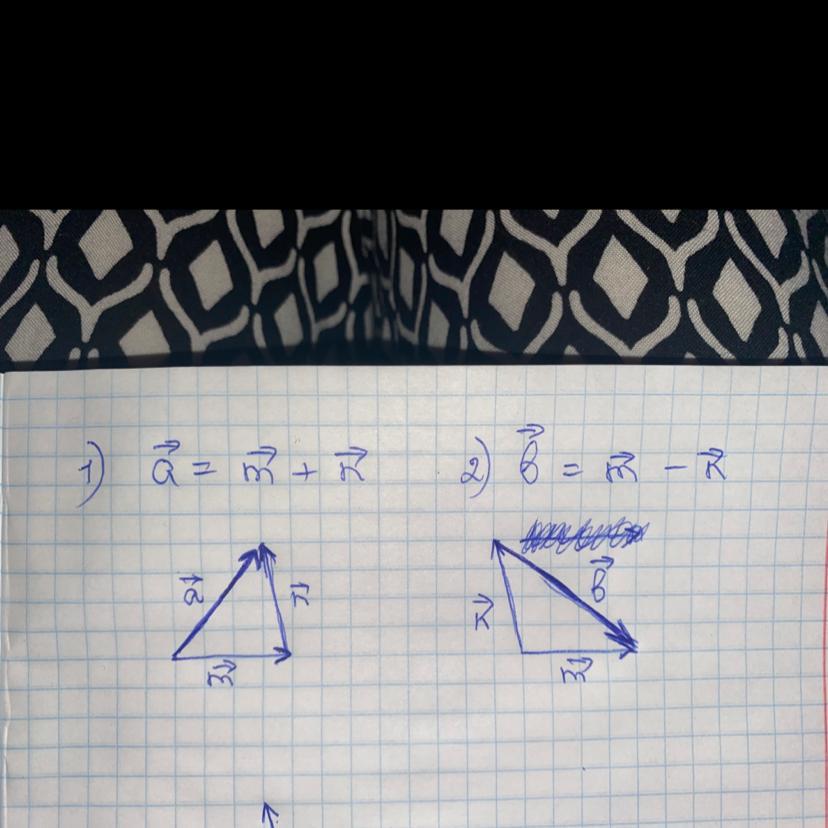
4. см. фото
5. 1) -1
2) 4
6. Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by = 0 · (-3) + (-2) · 3 = 0 - 6 = -6
Найдем длины векторов:
|a| = √ax2 + ay2 = √02 + (-2)2 = √0 + 4 = √4 = 2
|b| = √bx2 + by2 = √(-3)2 + 32 = √9 + 9 = √18 = 3√2
Найдем угол между векторами:
cos α = a · b / |a||b|
cos α = -6 / 2* 3√2 = - √2 / 2
угол равен 135 градусов
7. Поскольку AB = {Bx - Ax; By - Ay} = {5 - 3; 6 - 4} = {2; 2} , то AB = CD и АB || CD
Значит, данный четырёхугольник — параллелограмм, а т.к.
AD = {Dx - Ax; Dy - Ay} = {5 - 3; 2 - 4} = {2; -2},
то AB*AD = 2*2 + 2*(-2) = 4 -4 = 0
то AB перпендикулярно AD. Поэтому данный четырёхугольник — прямоугольник.
Осталось доказать, что равны его соседние стороны. Действительно, по формуле для расстояния между двумя точками
AD = √(2^2 + (-2)^2)= √(4 + 4)= √8 = 2√2
AB = √(2^2 + 2^2)= √(4 + 4) = √8 = 2√2
Что и требовалось доказать.
Ответ: AB = {5; -12}
2. a · b = ax · bx + ay · by = 5 · 4 + (-2) · 3 = 20 - 6 = 14
3.
1) м = (4;-2) + (1;5) = (5;3)
2) м = 3(4;-2) - 4(1;5) = (12;-6) - (4;20) = (8;-26)
4. см. фото
5. 1) -1
2) 4
6. Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by = 0 · (-3) + (-2) · 3 = 0 - 6 = -6
Найдем длины векторов:
|a| = √ax2 + ay2 = √02 + (-2)2 = √0 + 4 = √4 = 2
|b| = √bx2 + by2 = √(-3)2 + 32 = √9 + 9 = √18 = 3√2
Найдем угол между векторами:
cos α = a · b / |a||b|
cos α = -6 / 2* 3√2 = - √2 / 2
угол равен 135 градусов
7. Поскольку AB = {Bx - Ax; By - Ay} = {5 - 3; 6 - 4} = {2; 2} , то AB = CD и АB || CD
Значит, данный четырёхугольник — параллелограмм, а т.к.
AD = {Dx - Ax; Dy - Ay} = {5 - 3; 2 - 4} = {2; -2},
то AB*AD = 2*2 + 2*(-2) = 4 -4 = 0
то AB перпендикулярно AD. Поэтому данный четырёхугольник — прямоугольник.
Осталось доказать, что равны его соседние стороны. Действительно, по формуле для расстояния между двумя точками
AD = √(2^2 + (-2)^2)= √(4 + 4)= √8 = 2√2
AB = √(2^2 + 2^2)= √(4 + 4) = √8 = 2√2
Что и требовалось доказать.
Приложения:
gladkih65:
спасибо
отметь как лучшее, пожалуйста
Похожие вопросы
Предмет: Українська мова,
автор: irinarusu86
Предмет: Русский язык,
автор: 8888galina888
Предмет: Русский язык,
автор: 220484
Предмет: Алгебра,
автор: KRLsPage