Question

Задача 4.

Даны окружность с центрам О радиусом 4,5 см и точка А. ИЗ точки А проведены две касательные к окружности. Найти угол между ними, если ОА=9см .​

Answer 1

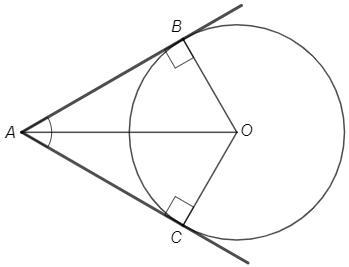
B, C - точки касания

OB=OC =4,5 (радиусы)

Радиус в точку касания перпендикулярен касательной, ∠OBA=∠OCA=90°

△AOB=△AOC (по катету и гипотенузе) => ∠BAO=∠CAO

Доказали: касательные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

OB/OA =4,5/9 =1/2

В треугольнике AOB катет OB равен половине гипотенузы OA, следовательно лежит против угла 30°.

∠BAO=30° => ∠BAC =30*2 =60°