Предмет: Математика,
автор: stragones
Помогите!Нужно вычеслить несобственный интеграл:
Приложения:
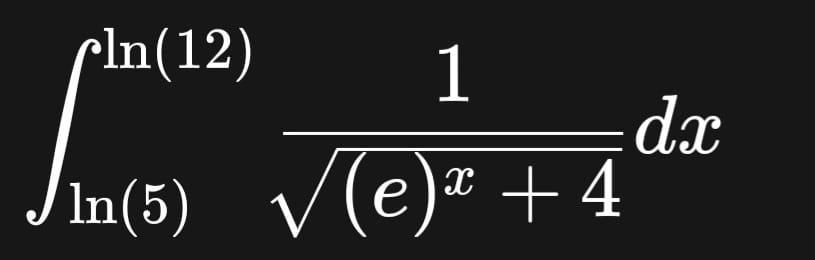
mionkaf1:
не похоже на несобственный интеграл
ага, обычный определенный интеграл....
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: madinamustafae
Предмет: Русский язык,
автор: f4ceeee
Предмет: Русский язык,
автор: taalinka2002
Предмет: Английский язык,
автор: ПэрсикСладкий