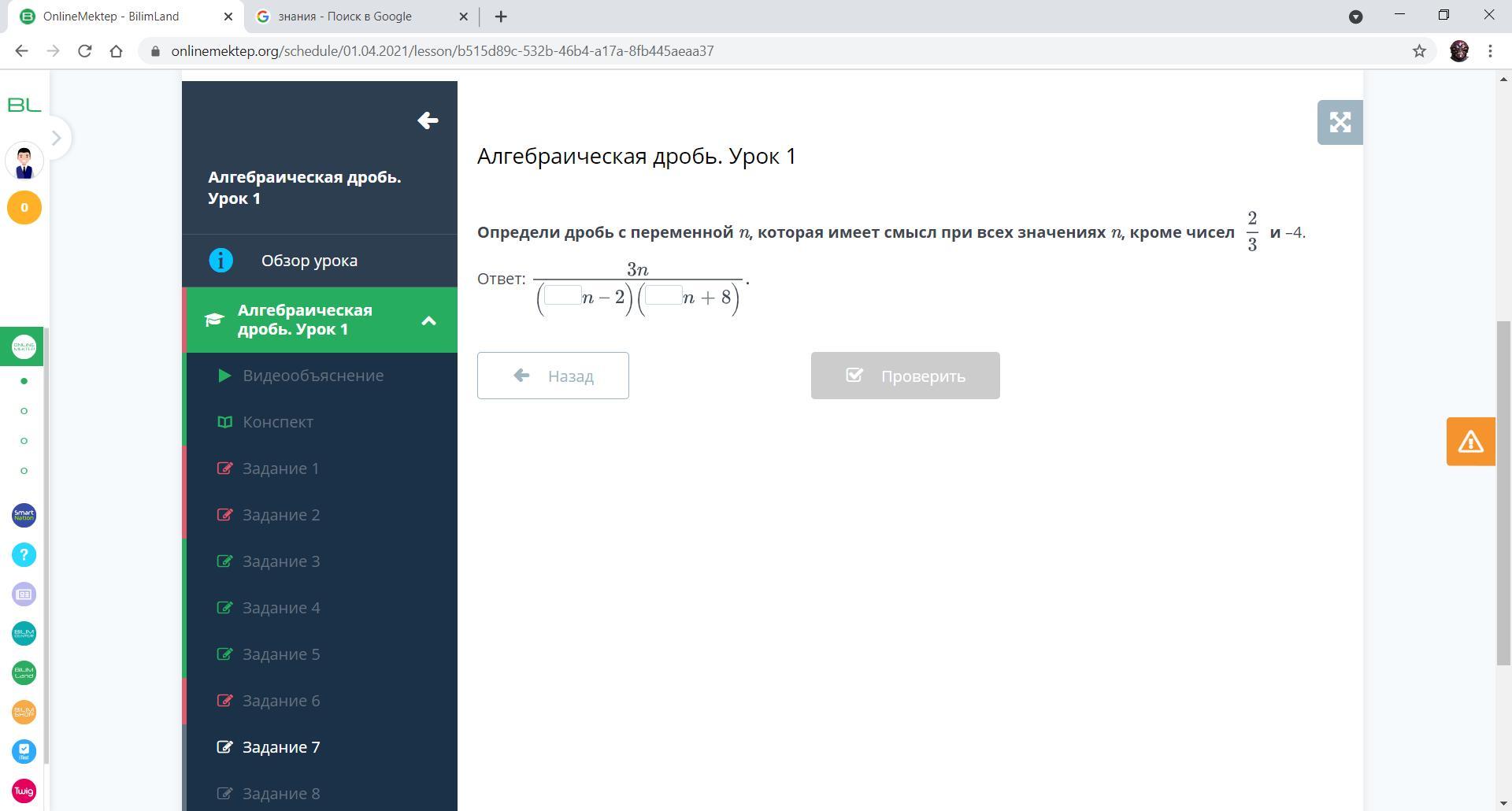
Определи дробь с переменной n, которая имеет смысл при всех значениях n, кроме чисел
и –4.
Ответы
Ответ: Возможны два решения:
1)
2)
Объяснение:
Алгебраическая дробь имеет смысл, когда знаменатель не равен нулю. В задаче обозначено, что дробь должна иметь смысл при всех n кроме 2/3 и -4, значит при этих n знаменатель должен обращаться в ноль.
Пусть a и b - это коэффициенты, которые необходимо найти. То есть нужна пара (a;b), при которой (an-2)(bn+8)=0 и в точке n=2/3, и в точке n=-4. Произведение двух множителей равно нулю, когда один из множителей равен нулю. Если один множитель равен нулю в одной точке, то в другой точке он равен нулю уже не будет - значит необходимо, чтобы в другой точке был равен нулю другой множитель.
1) Рассмотрим случай, когда (an-2)=0 в точке n=2/3
a*2/3-2=0 ⇒ a=3
Тогда (bn+8)=0 должно быть верно в точке n=-4
b*(-4)+8=0 ⇒ b=2
Первое решение - пара (a;b)=(3;2)
2) Рассмотрим случай, когда (an-2)=0 в точке n=-4
a*(-4)-2=0 ⇒ a=-1/2
Тогда (bn+8)=0 должно быть верно в точке n=2/3
b*2/3+8=0 ⇒ b=-12
Второе решение - пара (a;b)=(-1/2;-12)