Question

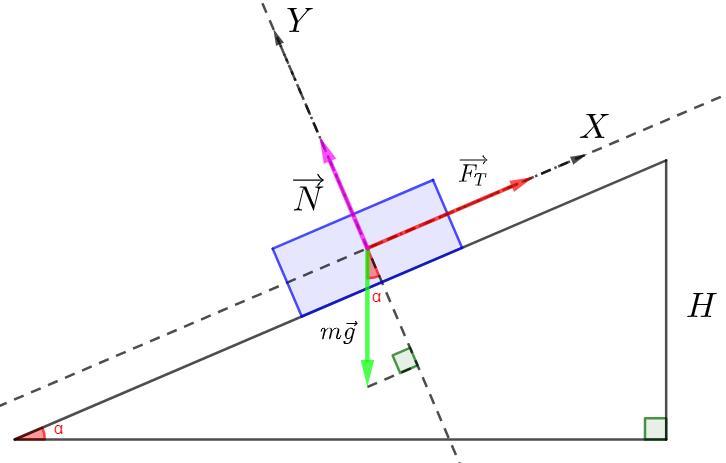
з вершини похилої площини висотою 10 м і кутом похилу 30 починає зісковзувати тіло. визначити швидкість тіла наприкінці спуску. коефіцієнт тертя тіла об площину дорівнює 0,1

Answer 1

Ответ:

$v_{k} \approx 12,9$ м/c

Примечание:

S - гіпотенуза трикутника

За означенням синуса в прямокутному трикутнику:

$\sin \alpha = \dfrac{H}{S} \Longrightarrow S = \dfrac{H}{\sin \alpha} = \dfrac{10}{\sin 30^{\circ} } = \dfrac{10}{0,5} = 20$ м.

Объяснение:

Дано:

H = 10 м

α = 30°

$\mu =$ 0,1

g = 10 м/c²

Знайти:

$v_{k} \ - \ ?$

----------------------------------

Розв'язання:

$m \vec{g} + \overrightarrow{N} +\overrightarrow{F_{T}} = m \vec{a}$ - за другим законом Ньютона

$OY: N - mg \cos \alpha =0; N = mg \cos \alpha;$

$F_{T} = \mu N = \mu mg \cos \alpha$

$A_{K} = A_{P} - A_{T};$

$\dfrac{mv_{k}^{2}}{2} = mgH - F_{T}S| \cdot 2$

$mv_{k}^{2} = 2mgH - 2F_{T}S$

$mv_{k}^{2} = 2mgH - 2S\mu mg \cos \alpha|:m$

$v_{k}^{2} = 2gH - 2\cdot\dfrac{H}{\sin \alpha} \cdot \mu g \cos \alpha$

$v_{k}^{2} = 2gH - 2gH \mu \ \rm ctg \ \alpha$

$v_{k}^{2} = 2gH(1 - \mu \cdot \rm ctg \ \alpha)$

$v_{k} = \sqrt{2gH(1 - \mu \cdot \rm ctg \ \alpha)}$

$v_{k} =$ √(2 * 10 м/c² * 10 м * (1 - 0,1 * √3)) ≈ 12,9 м/c

Відповідь: $v_{k} \approx 12,9$ м/c.