Предмет: Математика,
автор: lashroale3839
Помогите решить эти 3 задания,дам 60 баллов
Приложения:
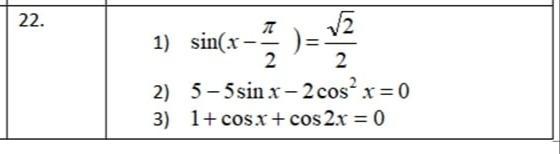
Ответы
Автор ответа:
1
1) Воспользуемся формулами:
2) Используем основное тригонометрическое тождество:
Квадратное уравнение с неизвестным .
3) Используем формулу косинуса двойного аргумента:
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: margaritorlov
Предмет: Окружающий мир,
автор: кукумака
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: sashakovachevip5r0ig
Предмет: Информатика,
автор: ДиваВиктория