Предмет: Геометрия,
автор: Home00000
Найди длины отрезков СРОЧНОООООООО
Приложения:
Ответы
Автор ответа:
0
Ответ:
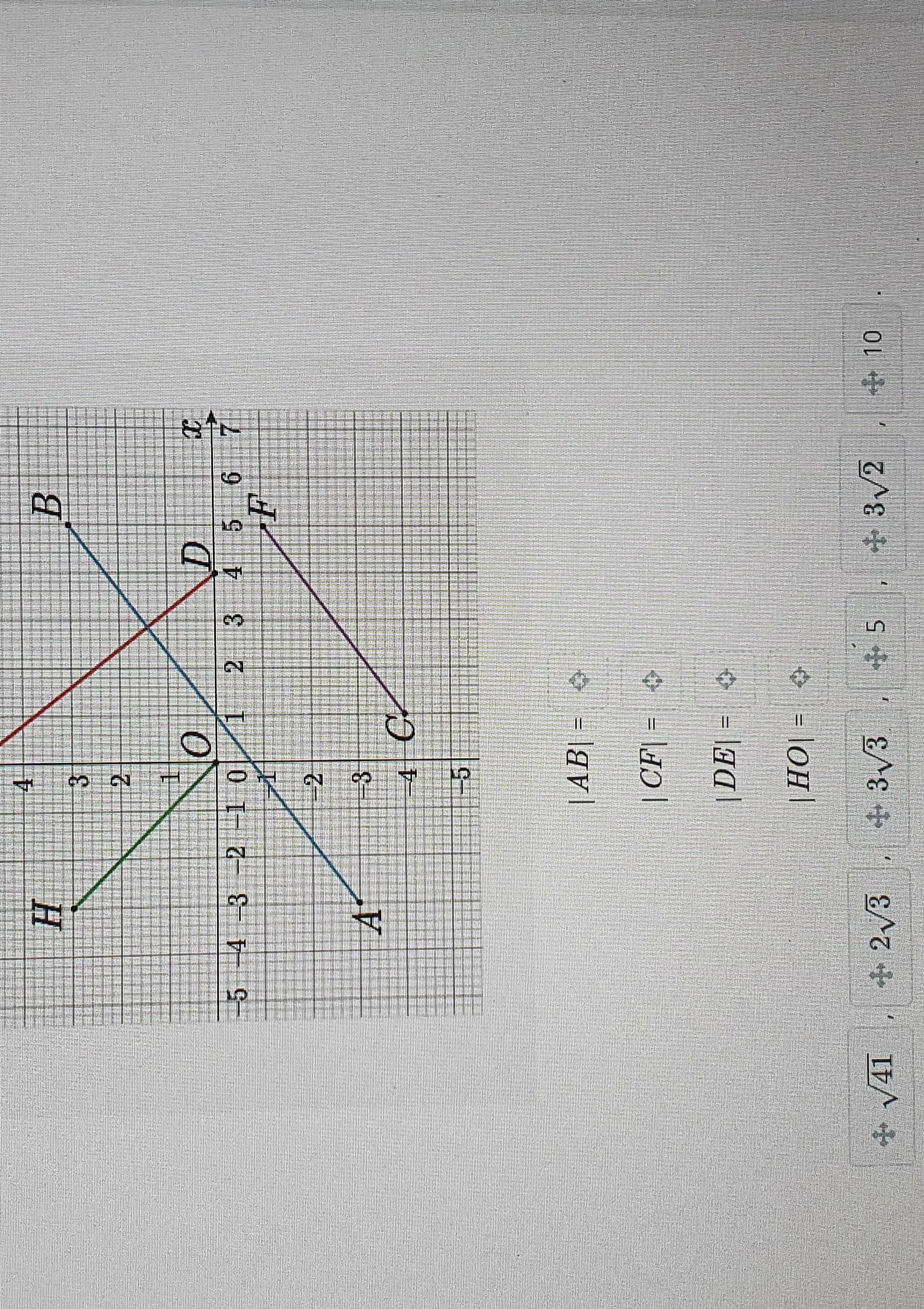
|AB| = 10
|CF| = 5
|DE| = √41
|HO| = 3√2
Объяснение:
- Расстояние между двумя точками А (х₁; у₁) и В (х₂; у₂) находится по формуле:
A (- 3; - 3), B (5; 3)
|AB| = 10
C (1; - 4), F (5; - 1)
|CF| = 5
D (4; 0), E (0; 5)
|DE| = √41
H (- 3; 3), O (0; 0)
|HO| = 3√2
Похожие вопросы
Предмет: Немецкий язык,
автор: вадим171
Предмет: Русский язык,
автор: lola1133
Предмет: Русский язык,
автор: arina200315
Предмет: Физика,
автор: Nic0las
Предмет: Литература,
автор: erd123