Предмет: Геометрия,
автор: jsnsnsnsnxjdhwpanzbz
Метод координат на плоскости. Растояние между двумя точками на плоскости по их координатам
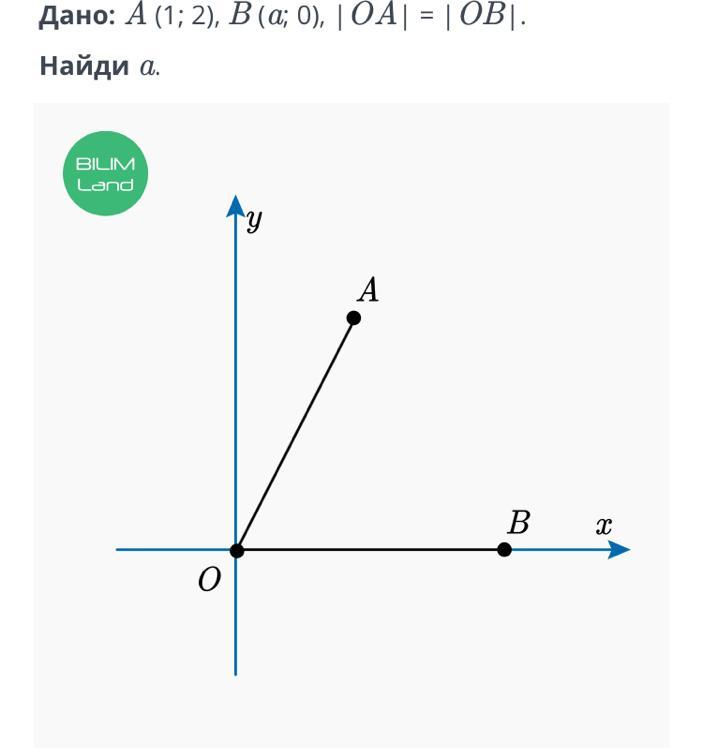
Дано: A (1; 2), B (a; 0), |OA| = |OB|.
Найди a.
Ответ: a =
Назад
Проверить
Приложения:
Ответы
Автор ответа:
1
Ответ:
а = √5
Объяснение:
Длина отрезка с координатами концов (х₁; у₁) и (х₂; у₂) вычисляется по формуле:
А (1; 2), В(а; 0)
Найдем квадрат длины отрезка |ОА|, О(0; 0):
|ОА|² = (1 - 0)² + (2 - 0)² = 1 + 4 = 5
Запишем квадрат длины отрезка ОВ:
|ОВ|² = (а - 0)² + (0 - 0)² = а²
Так как |ОА| = |ОВ|, получаем:
а² = 5
а = √5 или а = - √5
Так как точка В расположена на положительной полуоси Ох, то
а = √5
Похожие вопросы
Предмет: Русский язык,
автор: mary1695
Предмет: Окружающий мир,
автор: 89с52о70ф38и65я6
Предмет: Русский язык,
автор: УмнаяШишка
Предмет: Английский язык,
автор: AMARA11
Предмет: Русский язык,
автор: marinavik85