Question

Метод координат на плоскости. Растояние между двумя точками на плоскости по их координатам

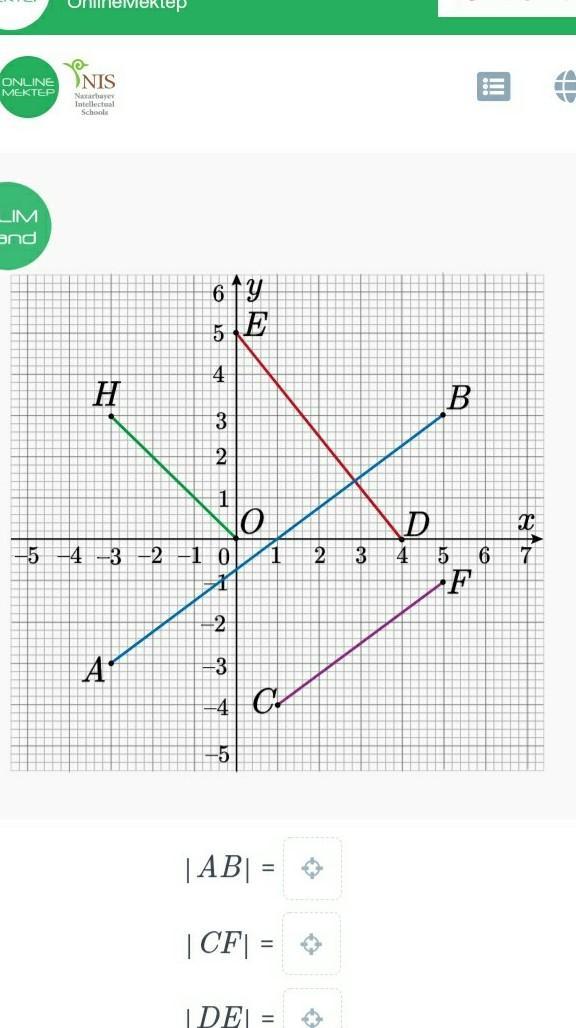
Найди длины отрезков.



|AB| =

|CF| =

|DE| =

|HO| =




​

Answer 1

Ответ:

$|AB| =10$

$|CF| =5$

$|DE| = \sqrt{41}$

$|HO| =3\sqrt{2}$

                                             Объяснение:

Формула расстояния между двумя точками, имеющими координаты (х₁; у₁) и (х₂; у₂):

$|AB| = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Чтобы определить координаты точки по рисунку, нужно опустить из нее перпендикуляры на оси. Число в основании перпендикуляра на ось х (вертикального) соответствует абсциссе точки, а число в основании перпендикуляра на ось у (горизонтального) — ее ординате.

Если точка лежит на оси абсцисс, то ее ордината равна нулю, если точка лежит на оси ординат, то ее абсцисса равна нулю.

______________________

1)

Определим координаты концов отрезка AB:

А (-3; -3);

В (5; 3).

Вычислим длину отрезка АВ по формуле:

$|AB| = \sqrt{(5+3)^2+(3+3)^2}= \sqrt{8^2 + 6^2} = \sqrt{64+36} = \sqrt{100}=10$

$|AB| =10$

2)

Определим координаты концов отрезка CF:

C (1; -4);

F (5; -1).

Вычислим длину отрезка CF по формуле:

$|CF| = \sqrt{(5-1)^2+(-1+4)^2}= \sqrt{4^2 + 3^2} = \sqrt{16+9} = \sqrt{25}=5$

$|CF| =5$

3)

Определим координаты концов отрезка DE:

D (4; 0);

E (0; 5).

Вычислим длину отрезка DE по формуле:

$|DE| = \sqrt{(0-4)^2+(5-0)^2}= \sqrt{(-4)^2 + 5^2} = \sqrt{16+25} = \sqrt{41}$

$|DE| = \sqrt{41}$

4)

Определим координаты концов отрезка HO:

H (-3; 3);

O (0; 0).

Вычислим длину отрезка CF по формуле:

$|HO| = \sqrt{(0+3)^2+(0-3)^2}= \sqrt{3^2 + (-3)^2} = \sqrt{9+9} = \sqrt{18}=3\sqrt{2}$

$|HO| =3\sqrt{2}$