Question

ПРОШУ ПОМОГИТЕ
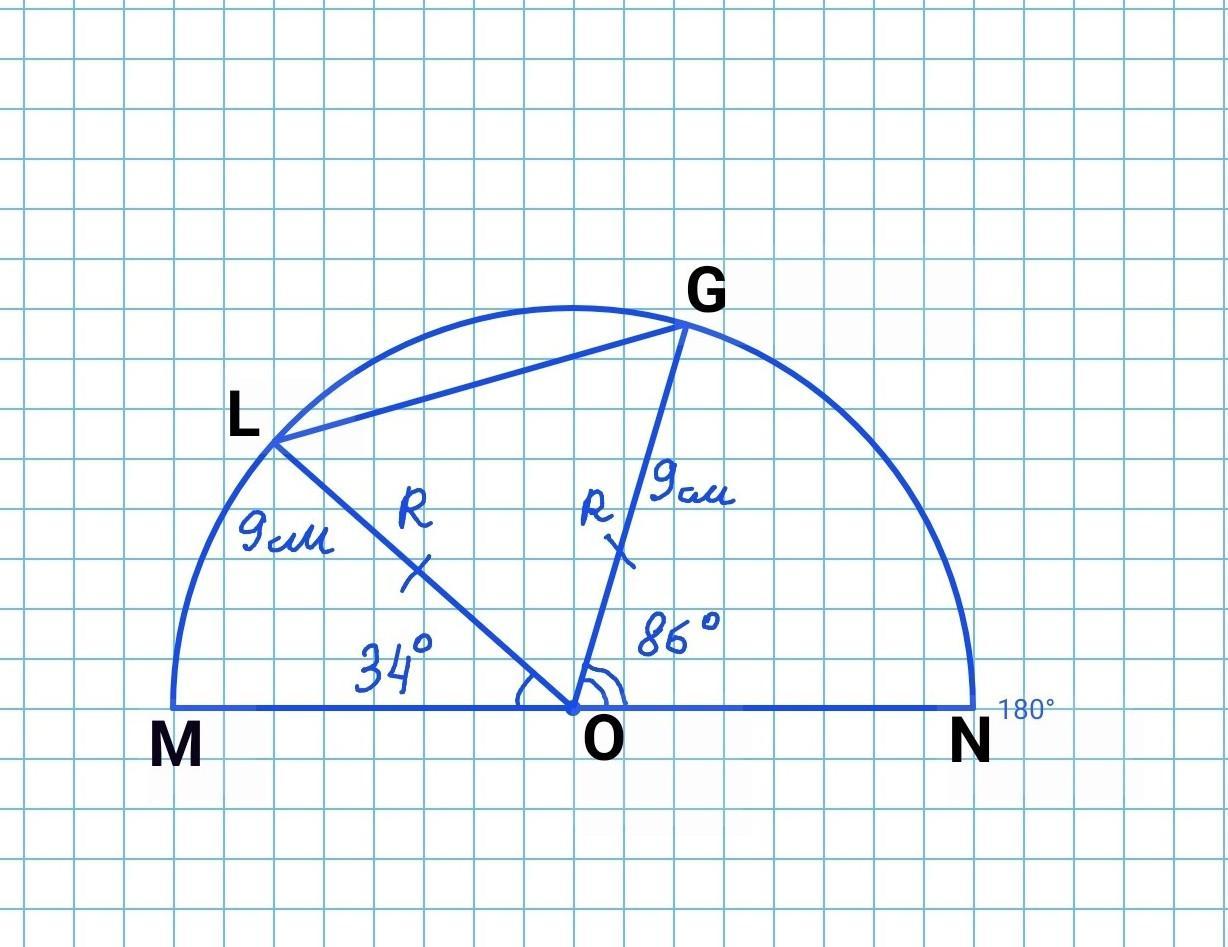
На полуокружности MN взяты точки L и G так, что ∠MOL = 34°, ∠GON = 86°. Найди хорду LG, если радиус окружности равен 9 см.

Answer 1

Ответ:

Хорда LG равна 9 см

Объяснение:

Хорда MN стягивающая дугу равную полуокружности, представляет собой развёрнутый угол. Градусная мера развёрнутого угла равна 180°.

Значит ∠MON=180°.

Тогда ∠LOG=∠MON-∠MOL-∠GON=180°-34°-86°=60°.

Рассмотрим треугольник LOG.

Так как LO=OG, как радиусы окружности, то △LOG - равнобедренный.

В равнобедренном треугольнике углы при основании равны.

∠L=∠G=(180°-∠LOG):2=(180°-60°):2=60°,

Если в треугольнике все углы равны, то треугольник равносторонний.

Следовательно △LOG - равносторонний.

Значит LG=LO=OG=R=9см