Предмет: Геометрия,
автор: davidsoldat589
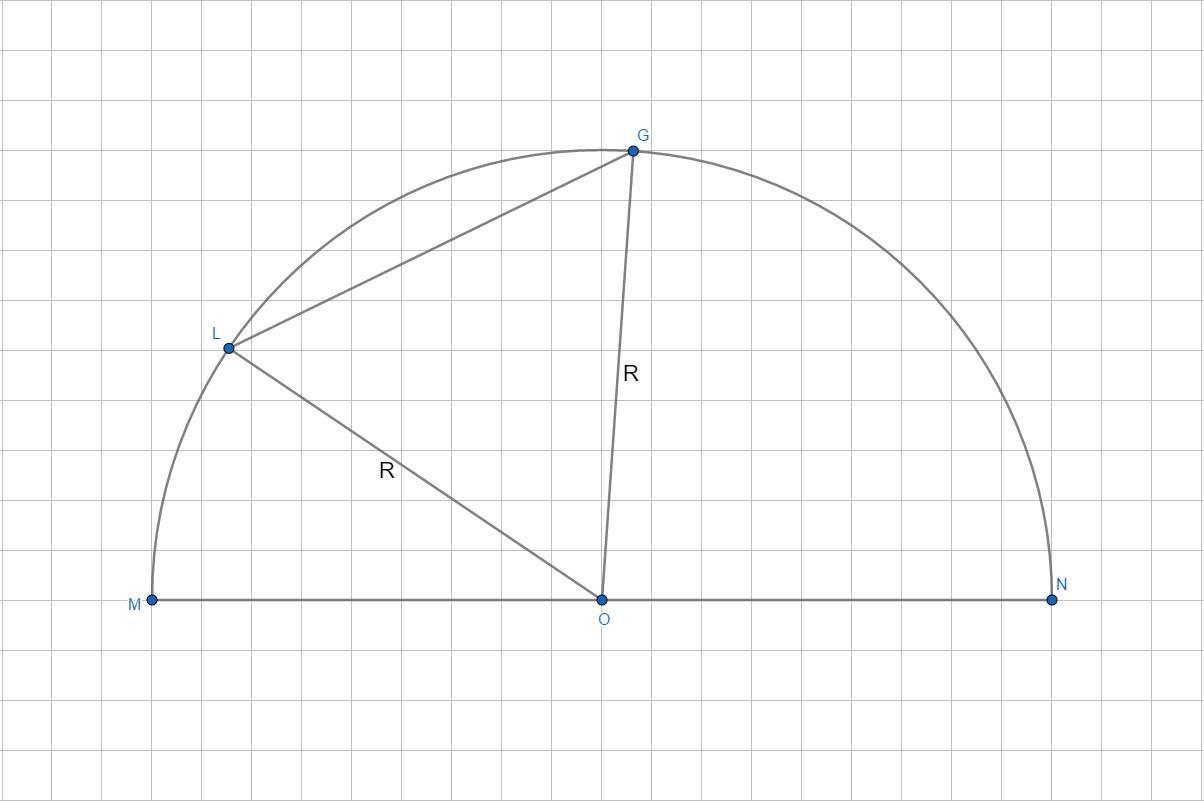
На полуокружности MN взяты точки L и G так, что ∠MOL = 34°, ∠GON = 86°. Найди хорду LG, если радиус окружности равен 9 см.
Ответ:
davidsoldat589:
Пожалуйста срочно
Короче ответ будет 9 я проверил
спасиьо ьолбшое
Ответы
Автор ответа:
1
Ответ:
- LG=9 см
Объяснение:
- Хорда, стягивающая дугу, равную полуокружности, представляет собой развернутый угол, градусная мера которого равна 180°.
Хорда MN стягивает дугу, равную полуокружности, значит, ∠MON=180° - развернутый.
Тогда ∠LOG=∠MON-∠MOL-∠GON=180°-34°-86°=60°.
- Все радиусы окружности равны между собой.
Треугольник ΔLOG - равнобедренный, т.к. OL=OG=9 см - как радиусы окружности. Тогда по свойству равнобедренного треугольника: ∠OLG=∠OGL.
- Теорема о сумме углов треугольника: Сумма углов треугольника равна 180°.
В ΔLOG из т. о сумме углов треугольника:
- Если у треугольника все углы равны, то этот треугольник равносторонний.
Получили, что ∠OLG=∠OGL=∠LOG=60°, значит, ΔLOG - равносторонний, следовательно, LG=OL=OG=9 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: плиз31
Предмет: Русский язык,
автор: vladyhsa
Предмет: Русский язык,
автор: MrTomasClap
Предмет: Алгебра,
автор: 46536ayf
Предмет: Русский язык,
автор: msvasilyva1