Окружность, круг, их элементы и части. Центральный угол. Урок 1
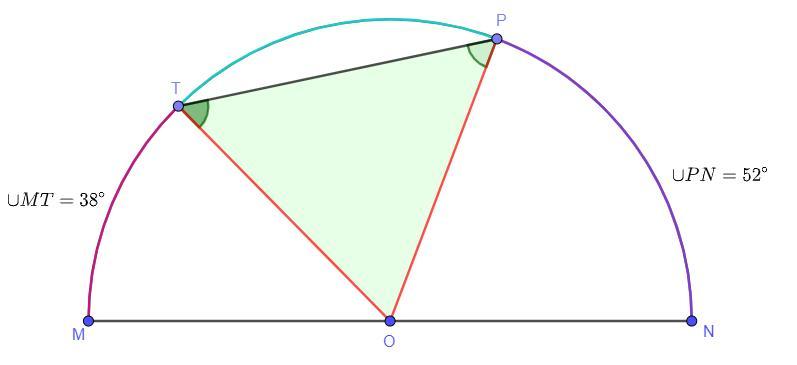
На полуокружности MN взяты точки T и P так, что ∪MT = 38°, ∪PN = 52°. Найди угол ∠PTO.
Ответы
Ответ:
∠PTO = 45°
Объяснение:
Дано: ∪MN - полуокружность, O - центр, ∪MT = 38°, ∪PN = 52°
Найти: ∠PTO - ?
Решение:
По определению градусная мера полуокружности 180°, тогда
∪MN = 180°.
∪MN = ∪MT + ∪PN + ∪PT ⇒ ∪PT = ∪MN - ∪MT - ∪PN = 180° - 38° - 52° =
= 90°.
По определению градусная мера дуги равняется центральному углу, который опирается на эту дугу, тогда угол ∠TOP = 90°.
Рассмотрим треугольник ΔPTO.
Треугольник ΔPTO - равнобедренный, так как TO = PO как радиусы, тогда по свойствам равнобедренного треугольника углы при основании равны (так как TO = PO как радиусы, то PT - основание), тогда ∠PTO = ∠TPO.
По теореме про сумму углов треугольника (ΔPTO):
∠PTO + ∠TPO + ∠TOP = 180°
∠PTO + ∠PTO + ∠TOP = 180°
2∠PTO + ∠TOP = 180°
2∠PTO = 180° - ∠TOP |*0,5
∠PTO = 0,5(180° - ∠TOP) = 90° - 0,5∠TOP = 90° - 0,5 * 90° =
= 90° - 45° = 45°