Даю 50 балов)) помогите пожалуйста)

Ответы
Пошаговое объяснение:
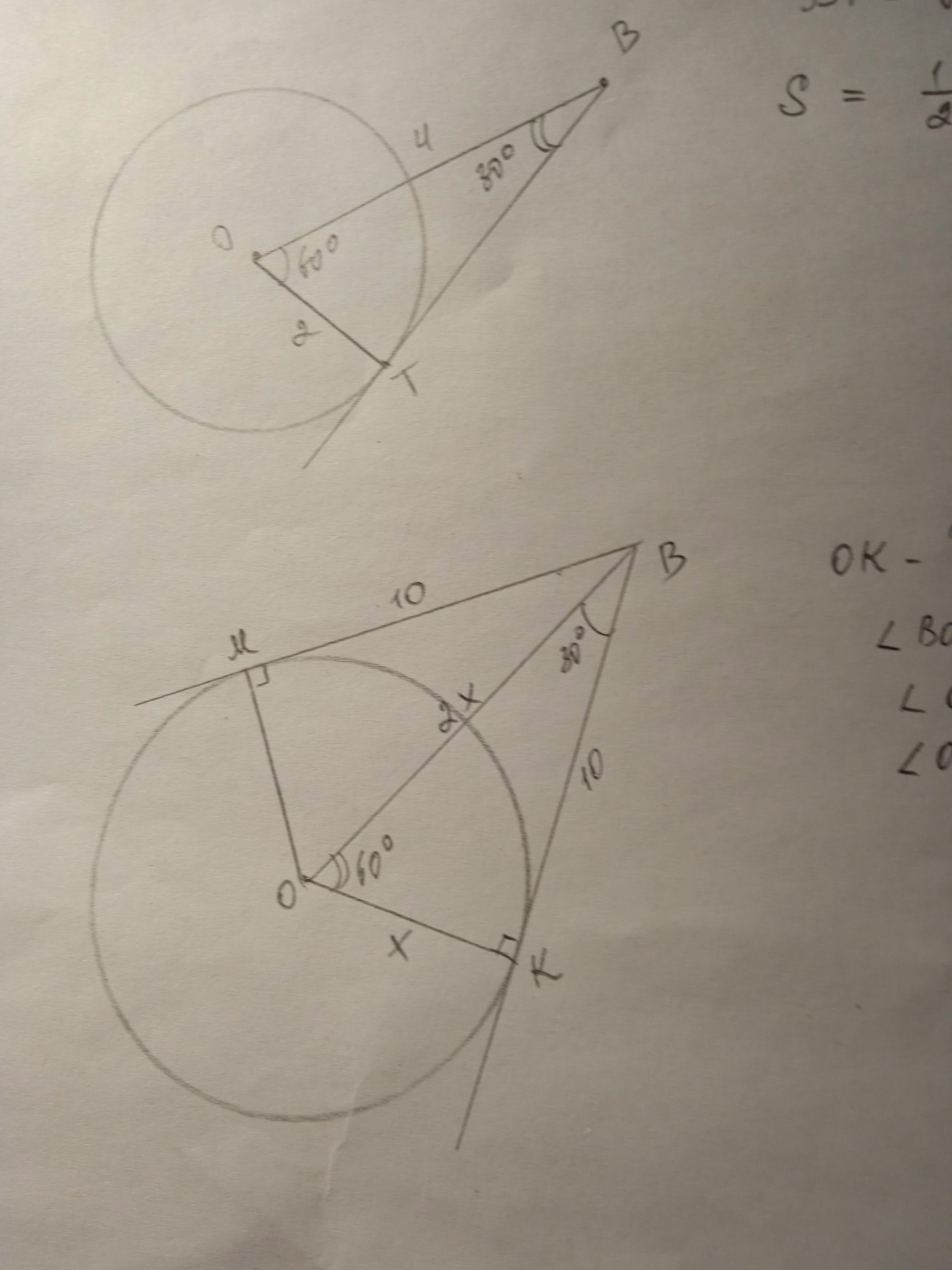
1. Угол между касательной и радиусом, проведенным в точку касания, равен 90°.
ΔОТВ - прямоугольный, ∠ОВТ=90-60=30° т.к. сумма острых углов прямоугольного треугольника составляет 90°
ОТ=1/2 ОВ как катет, лежащий против угла 30°
ОВ=2ОТ=4 см.
S=1/2 * ОТ * ОВ * sinO=1/2 * 2 * 4 * √3/2 = 2√3 см²
2. Угол между касательной и радиусом, проведенным в точку касания, равен 90°. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
ΔВОМ=ΔВОК; ∠ОВМ=∠ОВК=30°; ∠ВОМ=90-30=60°; ∠ОМВ=90°.
ВК=ВМ=10 см
ОК=1/2 ОВ как катет, лежащий против угла 30°. Пусть ОК=х см, тогда ОВ=2х см. По теореме Пифагора
(2х)²+х²=10²; 4х²+х²=100; 5х²=100; х²=20; х=√10=2√5 см
ОК=2√5 см; ОВ=2 * 2√5 = 4√5 см.