Question

правильная четырехугольная пирамида, со стороной основания равной $\sqrt{2}$. Ребро с основанием образует угол 30 градусов
1)найдите объём пирамиды
2)какой величины угол образуют сторона пирамиды с основанием

Answer 1

Правильная пирамида - в основании квадрат, вершина проецируется в центр описанной окружности основания.

Центр описанной окружности квадрата - пересечение диагоналей.

Диагонали квадрата равны, перпендикулярны, точкой пересечения делятся пополам.

SO⊥(ABC)

SAO=30

AO =AB cos45 =1

SO =AO tg30 =1/√3

Sосн =AB^2 =2

V =1/3 *Sосн *SO =2√3/9

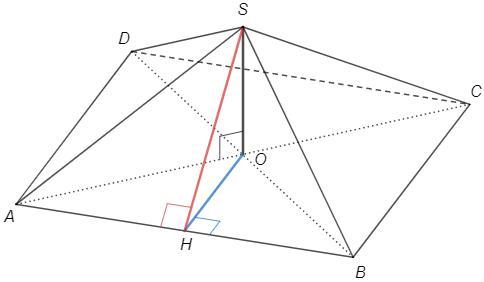
SO⊥(ABC), OH⊥AB => SH⊥AB (т о трех перпендикулярах)

∠SHO - линейный угол двугранного угла SABC

OH =AB/2 =1/√2

tg(SHO) =SO/OH =√(2/3) => ∠SHO =arctg(√(2/3)) ~39,23°