Предмет: Алгебра,
автор: innakuzmina48
Способ интегрирования по частям
Приложения:
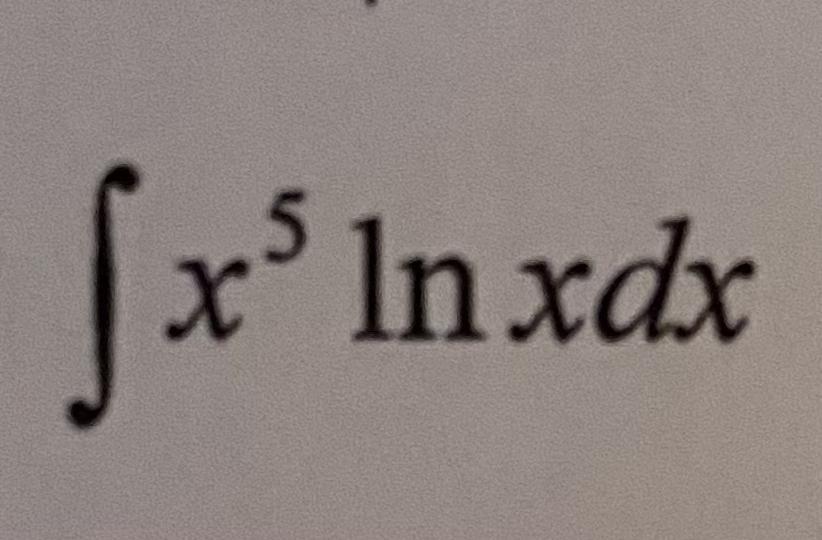
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: орксе
Предмет: Английский язык,
автор: shokoladMilka
Предмет: Английский язык,
автор: ALinaKacha
Предмет: Алгебра,
автор: irishakazakova
Предмет: Литература,
автор: Lisatoombs9