Предмет: Алгебра,
автор: jeremiahvaleska
cosπ/6-√3tg60°/sinπ/6+cos60°
Приложения:
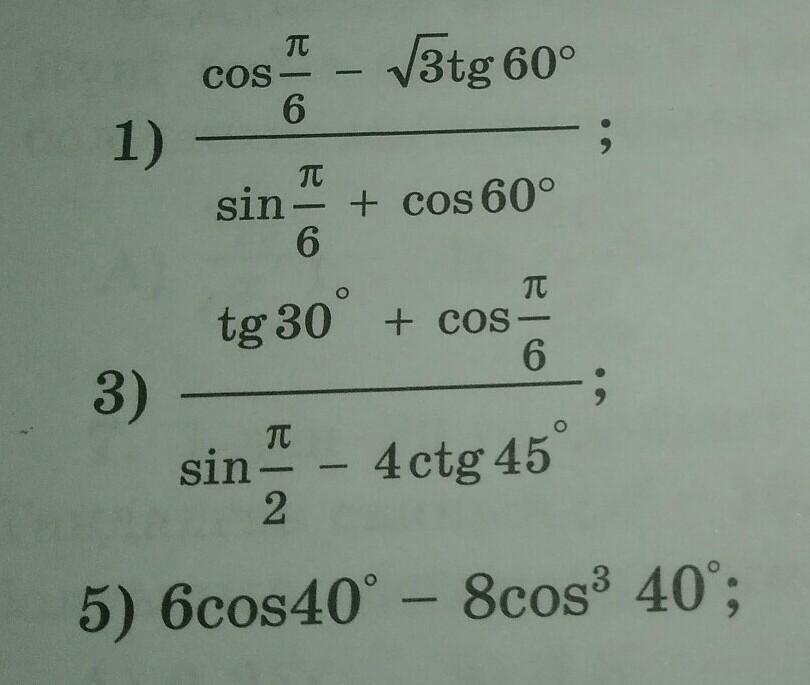
Ответы
Автор ответа:
3
При решении третьего задания применим формулу :
Cos3x = 4Cos³x - 3Cosx
Похожие вопросы
Предмет: Английский язык,
автор: vlasenko2003
Предмет: Русский язык,
автор: аслг
Предмет: Українська мова,
автор: knyazeva2
Предмет: Окружающий мир,
автор: alina2005g
Предмет: Окружающий мир,
автор: 123kir123