Предмет: Математика,
автор: sofija1511
Я нуждаюсь в помощи...Единственное, что мне тут не понятно, это то, как решить задачу под номером 3...Я уже всё перепробовала наверноe, но не получается как в ответах.(a=b= ~1,1; (угол Альфа)=(угол Бета) = 45°)Это задание оценочное и я не знаю, что мне делать.../Я пробовала находить h(b) из формулы S=c×h/2, я просто уже не знаю, что делать/
Приложения:

oksana12ocozigbf:
Попробуй через формулу S=c2* sinB/4 тогда 0.64=1.6*1.6* sin2B/4 sin2B=1 тогда уголВ=45* и дальше. Добавить ответ не получается у меня...
Ошибка!!!S=c2* sin2B/4
я...я не понимаю
Ответы
Автор ответа:
0
Ответ:
По моему вот так решается ........
Приложения:
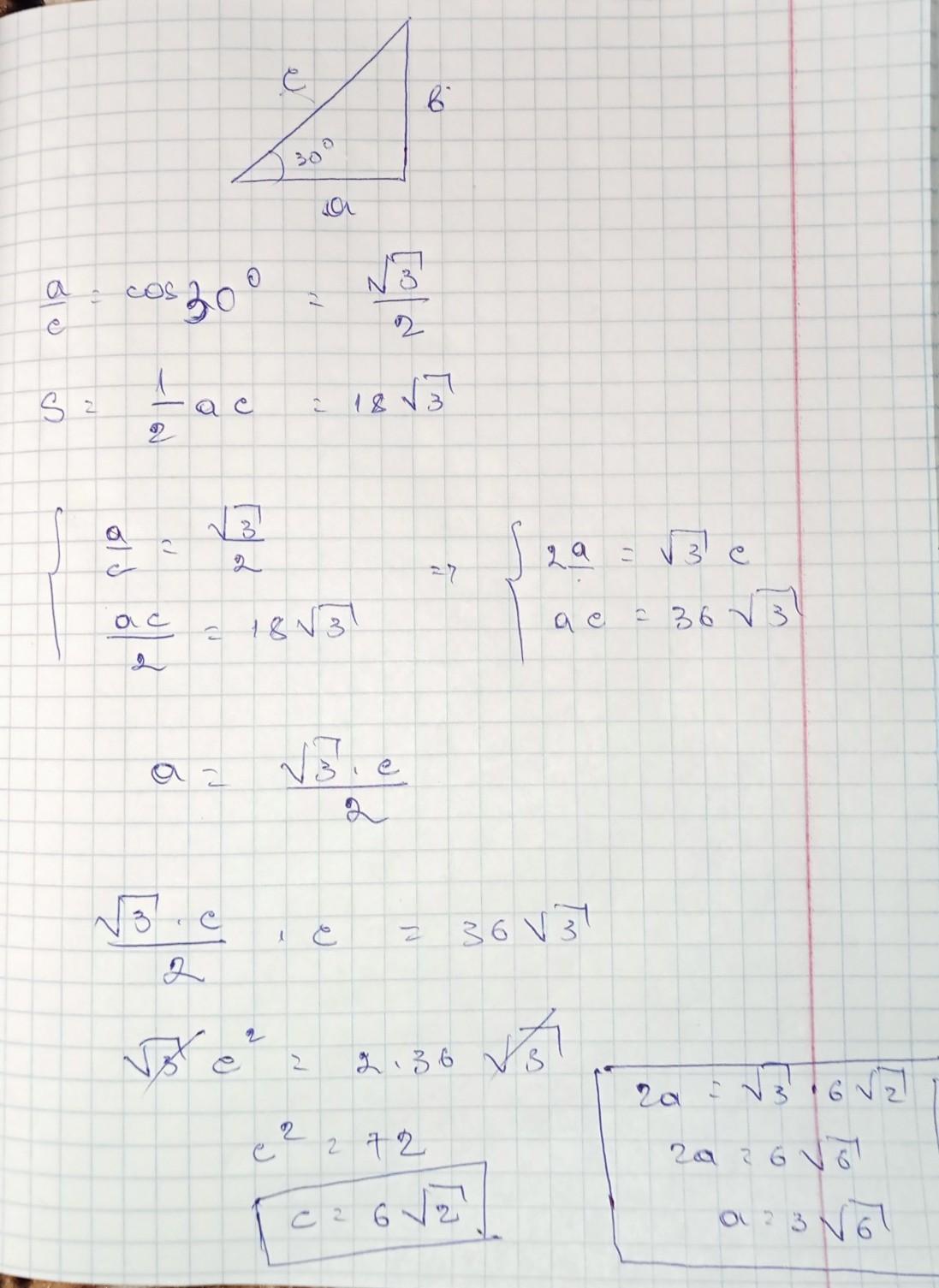
Автор ответа:
1
Т.к. a = b, углы равны 45 градусам
Похожие вопросы
Предмет: Русский язык,
автор: Стаснислав1
Предмет: Английский язык,
автор: serg060768
Предмет: Русский язык,
автор: nastea7thebest
Предмет: Окружающий мир,
автор: olgakrr
Предмет: Математика,
автор: elinafarkhadova