Предмет: Математика,
автор: angelina0312199985
Помогите пожалуйста решить под номером 8)
Приложения:

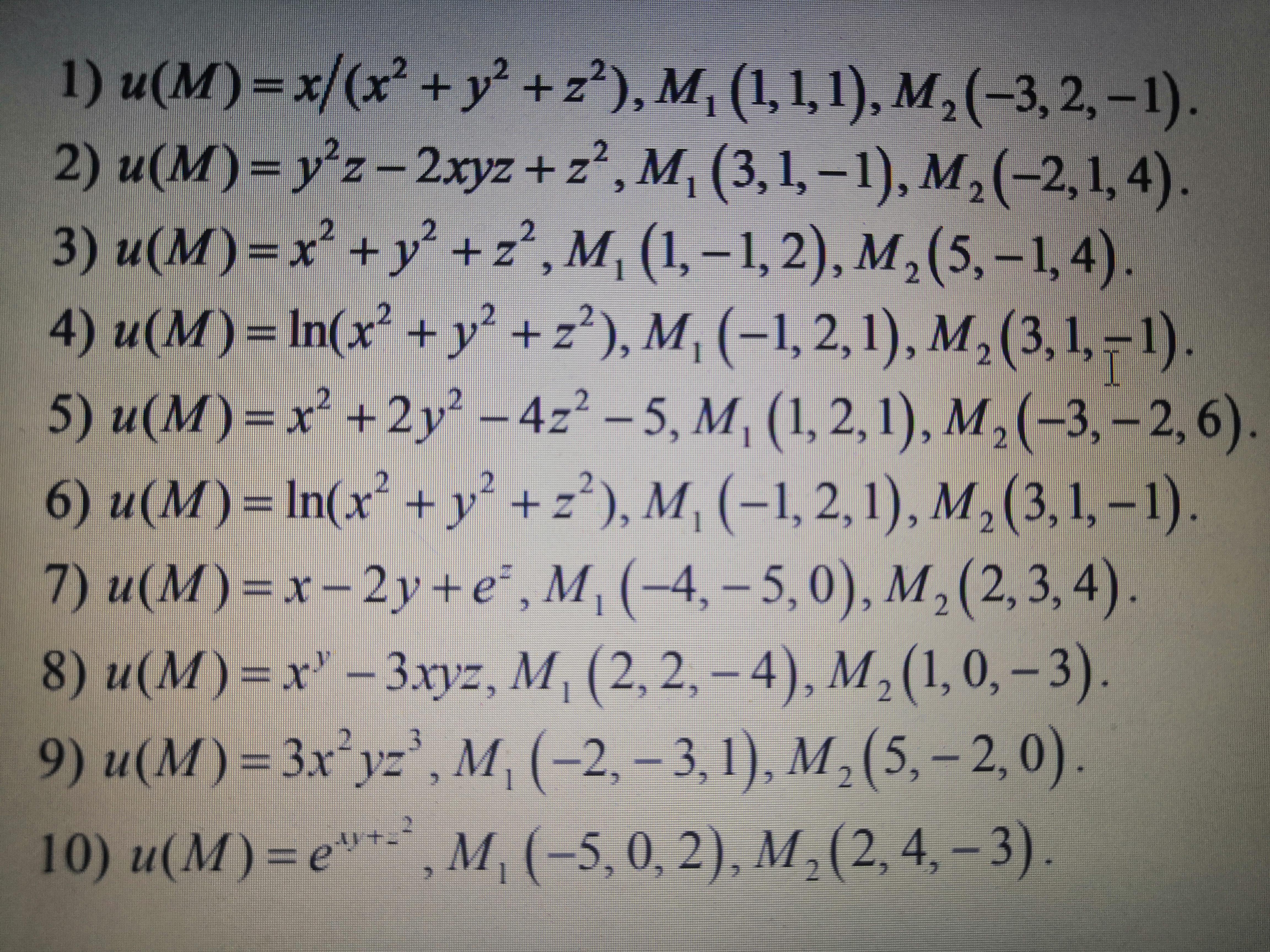
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
сначала вектор
a) производная в точке М1 по направлению вектора а(7;1;-1).
функция в направлении вектора возрастает
б)
направление вектора-градиента задаётся его направляющими косинусами
Похожие вопросы
Предмет: Английский язык,
автор: nicksuper554
Предмет: Русский язык,
автор: anastasiyakoro8
Предмет: Окружающий мир,
автор: dmitriykiselev1
Предмет: Математика,
автор: Матвей8802