Предмет: Геометрия,
автор: ernurumerbekov400
Диаганаль куба равна 1 см. Найдите ребра этого куба.
Ответы
Автор ответа:
0
Ответ:
см
Объяснение:
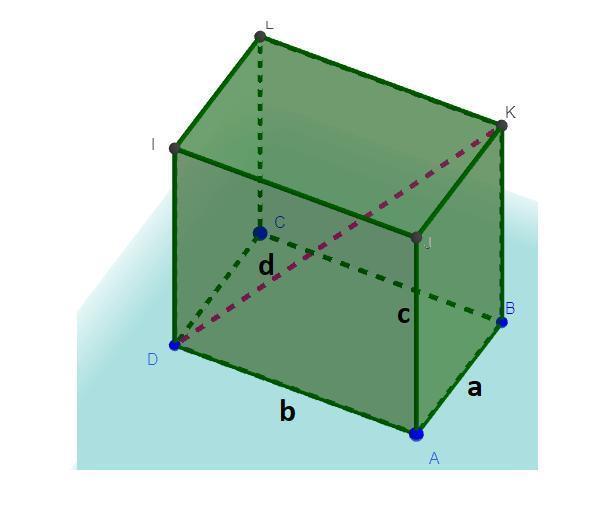
Пусть a,b,c - длины различных ребер выходящей из одной вершины.
По свойствам куба все его ребра равны, тогда a = b = c.
Пусть главная диагональ параллелепипеда d, тогда по формуле:
По условию d = 1 см.
см.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: solomiapuple
Предмет: Английский язык,
автор: Laa1Vika
Предмет: Українська література,
автор: irina241083
Предмет: Математика,
автор: Karina14544
Предмет: Химия,
автор: alinamelnikova7