Предмет: Математика,
автор: kgalanchenko
Вычислить криволинейевй интеграл 2-го рода?
Приложения:
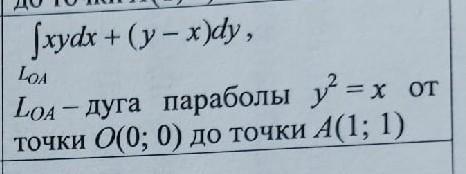
Ответы
Автор ответа:
0
Предположим, что кривая
C
задана векторной функцией
r
=
r
(
s
)
,
0
≤
s
≤
S
,
где переменная
s
− длина дуги кривой. Тогда производная векторной функции
d
r
d
t
=
τ
=
(
cos
α
,
cos
β
,
cos
γ
)
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок
1
).
В приведенной выше формуле
α
,
β
и
γ
− углы между касательной и положительными направлениями осей
O
x
,
O
y
и
O
z
,
соответственно.
Рис.1
Рис.2
Введем векторную функцию
F
(
P
,
Q
,
R
)
,
определенную на кривой
C
,
так, чтобы для скалярной функции
F
⋅
τ
=
P
cos
α
+
Q
cos
β
+
R
cos
γ
существовал криволинейный интеграл
∫
C
(
F
⋅
τ
)
d
s
.
Такой интеграл
∫
C
(
F
⋅
τ
)
d
s
называется криволинейным интегралом второго рода от векторной функции
F
вдоль кривой
C
и обозначается как
∫
C
P
d
x
+
Q
d
y
+
R
d
z
.
Таким образом, по определению,
∫
C
P
d
x
+
Q
d
y
+
R
d
z
=
S
∫
0
(
P
cos
α
+
Q
cos
β
+
R
cos
γ
)
d
s
,
где
τ
(
cos
α
,
cos
β
,
cos
γ
)
− единичный вектор касательной к кривой
C
.
Последнюю формулу можно переписать также в векторной форме:
∫
C
(
F
⋅
d
r
)
=
S
∫
0
(
F
(
r
(
s
)
)
⋅
τ
)
d
s
,
где
d
r
=
(
d
x
,
d
y
,
d
z
)
.
Если кривая
C
лежит в плоскости
O
x
y
,
то полагая
R
=
0
получаем
∫
C
P
d
x
+
Q
d
y
=
S
∫
0
(
P
cos
α
+
Q
cos
β
)
d
s
.
Свойства криволинейного интеграла второго рода
Криволинейный интеграл
I
I
рода обладает следующими свойствами:
Пусть
C
обозначает кривую с началом в точке
A
и конечной точкой
B
.
Обозначим через
−
C
кривую противоположного направления − от
B
к
A
.
Тогда
∫
−
C
(
F
⋅
d
r
)
=
−
∫
C
(
F
⋅
d
r
)
;
Если
C
− объединение кривых
C
1
и
C
2
(рисунок
2
выше), то
∫
C
(
F
⋅
d
r
)
=
∫
C
1
∪
C
2
(
F
⋅
d
r
)
=
∫
C
1
(
F
⋅
d
r
)
+
∫
C
2
(
F
⋅
d
r
)
;
Если кривая
C
задана параметрически в виде
r
(
t
)
=
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
,
α
≤
t
≤
β
,
то
∫
C
P
d
x
+
Q
d
y
+
R
d
z
=
β
∫
α
[
P
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
x
d
t
+
Q
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
y
d
t
+
R
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
z
d
t
]
d
t
.
Если кривая
C
лежит в плоскости
O
x
y
и задана уравнением
y
=
f
(
x
)
(предполагается, что
R
=
0
и
t
=
x
), то последняя формула записывается в виде
∫
C
P
d
x
+
Q
d
y
=
b
∫
a
[
P
(
x
,
f
(
x
)
)
+
Q
(
x
,
f
(
x
)
)
d
f
d
x
]
d
x
.
C
задана векторной функцией
r
=
r
(
s
)
,
0
≤
s
≤
S
,
где переменная
s
− длина дуги кривой. Тогда производная векторной функции
d
r
d
t
=
τ
=
(
cos
α
,
cos
β
,
cos
γ
)
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок
1
).
В приведенной выше формуле
α
,
β
и
γ
− углы между касательной и положительными направлениями осей
O
x
,
O
y
и
O
z
,
соответственно.
Рис.1
Рис.2
Введем векторную функцию
F
(
P
,
Q
,
R
)
,
определенную на кривой
C
,
так, чтобы для скалярной функции
F
⋅
τ
=
P
cos
α
+
Q
cos
β
+
R
cos
γ
существовал криволинейный интеграл
∫
C
(
F
⋅
τ
)
d
s
.
Такой интеграл
∫
C
(
F
⋅
τ
)
d
s
называется криволинейным интегралом второго рода от векторной функции
F
вдоль кривой
C
и обозначается как
∫
C
P
d
x
+
Q
d
y
+
R
d
z
.
Таким образом, по определению,
∫
C
P
d
x
+
Q
d
y
+
R
d
z
=
S
∫
0
(
P
cos
α
+
Q
cos
β
+
R
cos
γ
)
d
s
,
где
τ
(
cos
α
,
cos
β
,
cos
γ
)
− единичный вектор касательной к кривой
C
.
Последнюю формулу можно переписать также в векторной форме:
∫
C
(
F
⋅
d
r
)
=
S
∫
0
(
F
(
r
(
s
)
)
⋅
τ
)
d
s
,
где
d
r
=
(
d
x
,
d
y
,
d
z
)
.
Если кривая
C
лежит в плоскости
O
x
y
,
то полагая
R
=
0
получаем
∫
C
P
d
x
+
Q
d
y
=
S
∫
0
(
P
cos
α
+
Q
cos
β
)
d
s
.
Свойства криволинейного интеграла второго рода
Криволинейный интеграл
I
I
рода обладает следующими свойствами:
Пусть
C
обозначает кривую с началом в точке
A
и конечной точкой
B
.
Обозначим через
−
C
кривую противоположного направления − от
B
к
A
.
Тогда
∫
−
C
(
F
⋅
d
r
)
=
−
∫
C
(
F
⋅
d
r
)
;
Если
C
− объединение кривых
C
1
и
C
2
(рисунок
2
выше), то
∫
C
(
F
⋅
d
r
)
=
∫
C
1
∪
C
2
(
F
⋅
d
r
)
=
∫
C
1
(
F
⋅
d
r
)
+
∫
C
2
(
F
⋅
d
r
)
;
Если кривая
C
задана параметрически в виде
r
(
t
)
=
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
,
α
≤
t
≤
β
,
то
∫
C
P
d
x
+
Q
d
y
+
R
d
z
=
β
∫
α
[
P
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
x
d
t
+
Q
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
y
d
t
+
R
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
d
z
d
t
]
d
t
.
Если кривая
C
лежит в плоскости
O
x
y
и задана уравнением
y
=
f
(
x
)
(предполагается, что
R
=
0
и
t
=
x
), то последняя формула записывается в виде
∫
C
P
d
x
+
Q
d
y
=
b
∫
a
[
P
(
x
,
f
(
x
)
)
+
Q
(
x
,
f
(
x
)
)
d
f
d
x
]
d
x
.
kgalanchenko:
спасибо канечно, а можно мне отправить это целым текстом. вы сами посмотрите, что отправили.
Похожие вопросы
Предмет: Русский язык,
автор: mihailgrishin75
Предмет: Українська мова,
автор: baddenikova
Предмет: Русский язык,
автор: iagodka10
Предмет: Алгебра,
автор: makis5670
Предмет: Математика,
автор: Shanon