Question

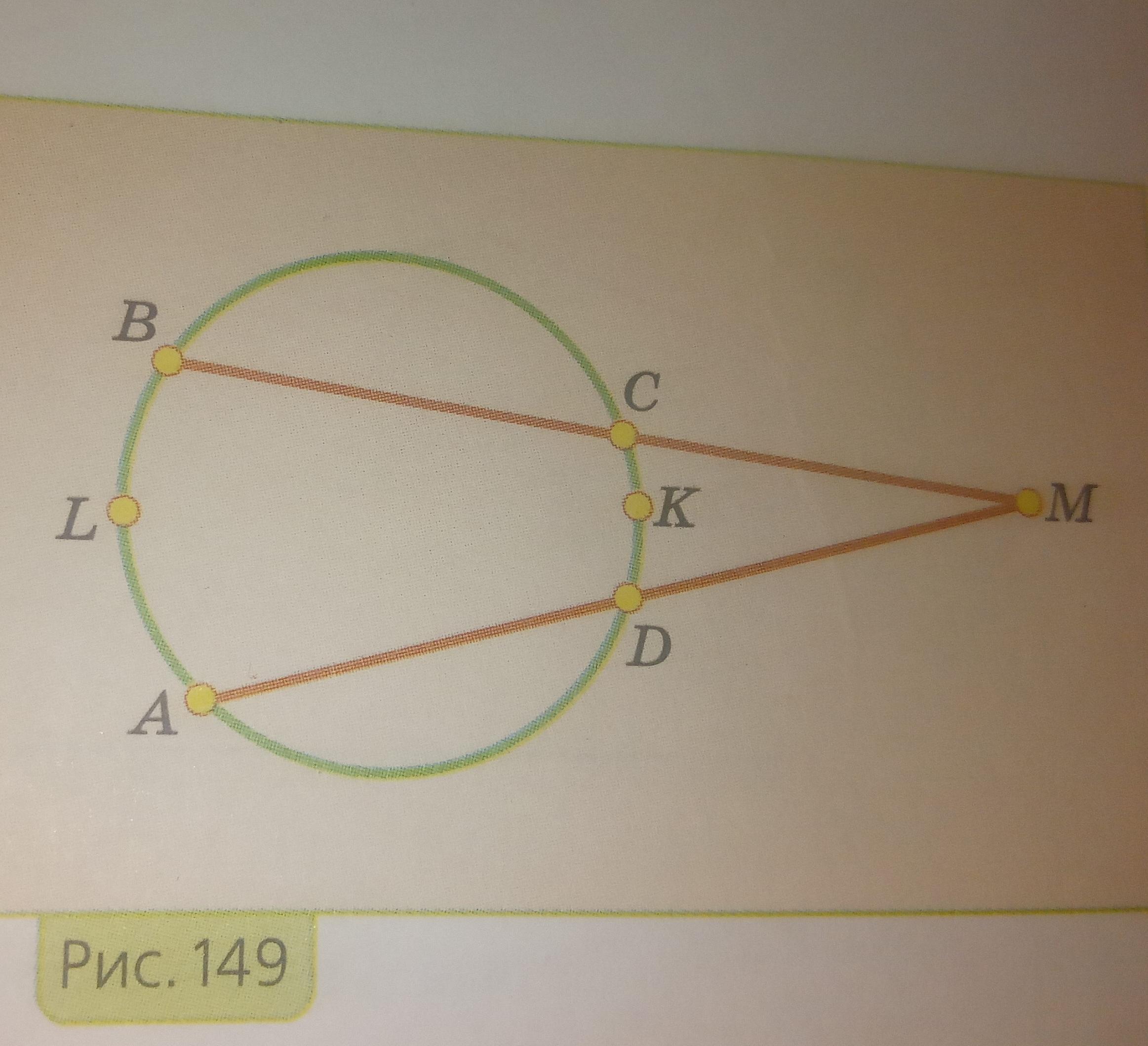
Исходя из рисунка 149 докажите что угол амв равен 1/2(дуга алб-дуга скд)

Answer 1

Ответ:

Объяснение:

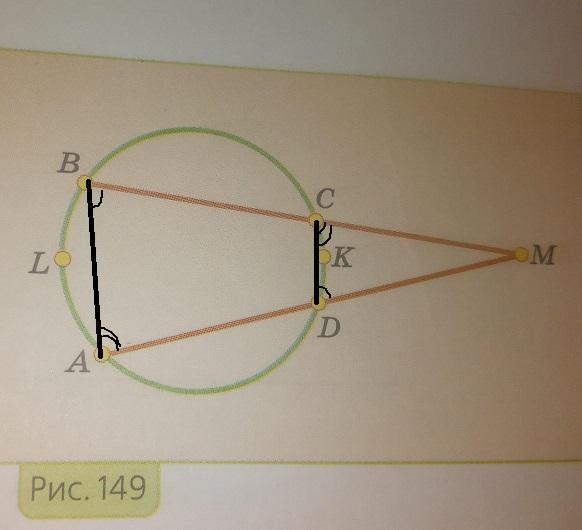
Соединим А и В, С и D. Четырехугольник ABCD - вписанный, значит <ABC+<ADC=180° и <CDM+<ADC=180°, значит <ABC=<CDM. Аналогично <BAD=<DCM.

Из тр-ка △CMD <CMD(AMB)=180-<CDM-<DCM=180-<ABC-<BAD

<ABC=1/2*(AD+CD); <BAD=1/2(BC+CD).

<AMB=180-1/2*(AD+CD)-1/2*(BC+CD)=180-1/2*(AD+CD+BC)-1/2*CD

Для дуг окружности можно записать:

AD+CD+BC=360-AB - подставим в последнее выражение:

<AMB=180-1/2*(360-АВ)-1/2*СD=180-180+1/2*АВ-1/2*СD=1/2*(AB-CD)=1/2*(ALB-CKD)