Предмет: Алгебра,
автор: sonarkhipova2003
Помогите пожалуйста✨
Приложения:
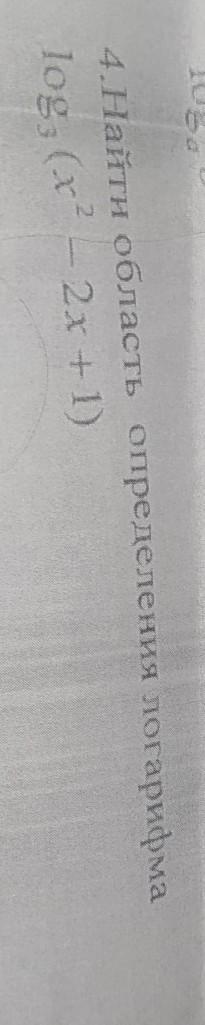
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Логарифм по основанию от числа
существует тогда и только тогда, когда
Таким образом, требуется, чтобы было положительным, ведь
уже удовлетворяет условию.
Пусть исходный логарифм это , тогда
, где
,
.
Тогда условие на это:
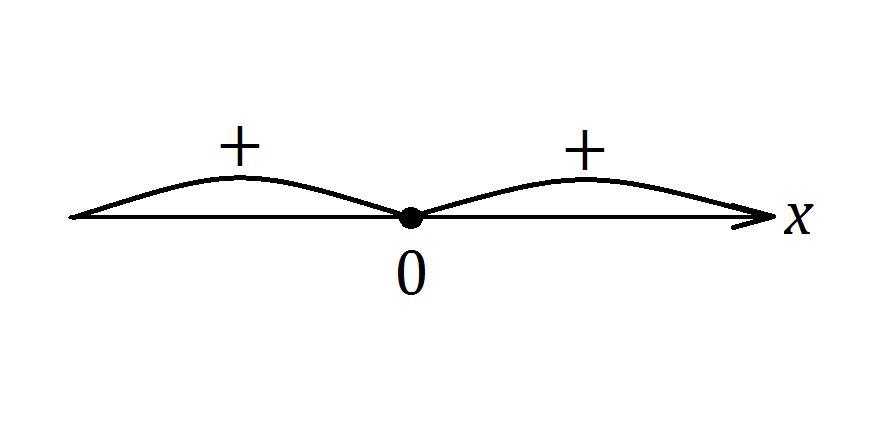
то есть у квадратного уравнения лишь один корень, то есть аргумент логарифма становится нулём единожды в точке пересечения функции под логарифмом с осью
. Решим неравенство далее:
Методом интервалов находим, что решением неравенства будет такое условие:
Получается, что не должен быть равным единице.
Областью определения логарифма и будет являться получившееся условие, то есть, в символьном виде,
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: persik23
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: ZeeDYT
Предмет: История,
автор: arts777
Предмет: Русский язык,
автор: Мармеладик9