Предмет: Алгебра,
автор: kate4534
Решите пожалуйста даю 23 бал
Номер 4,5,6
Приложения:
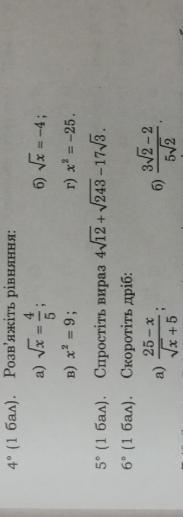
Ответы
Автор ответа:
2
Ответ:
4.
а)
б)
в)
г)
5.
6.
a)
б)
Объяснение:
4.
а)
б)
в)
г)
5.
6.
а)
б)
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Амили7
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Tatyana23457