Предмет: Алгебра,
автор: megamiha2401
Неравенство с логарифмом - решите пожалуйста подробно
Приложения:
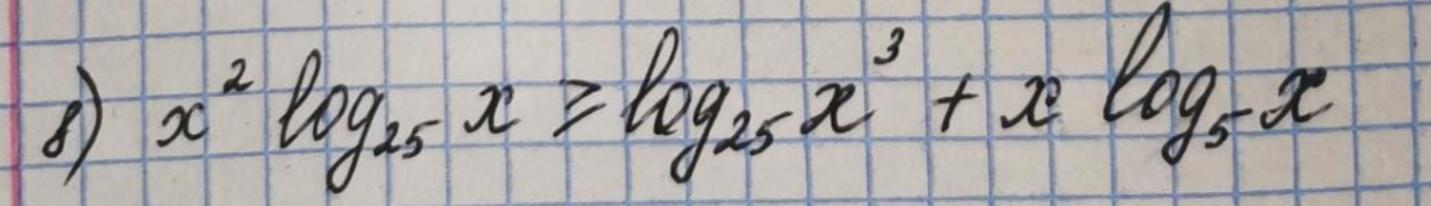
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: MashaBaimasova
Предмет: Английский язык,
автор: zueval2003
Предмет: Русский язык,
автор: Ромик777
Предмет: История,
автор: Ivanpomogite9
Предмет: Математика,
автор: okeu2