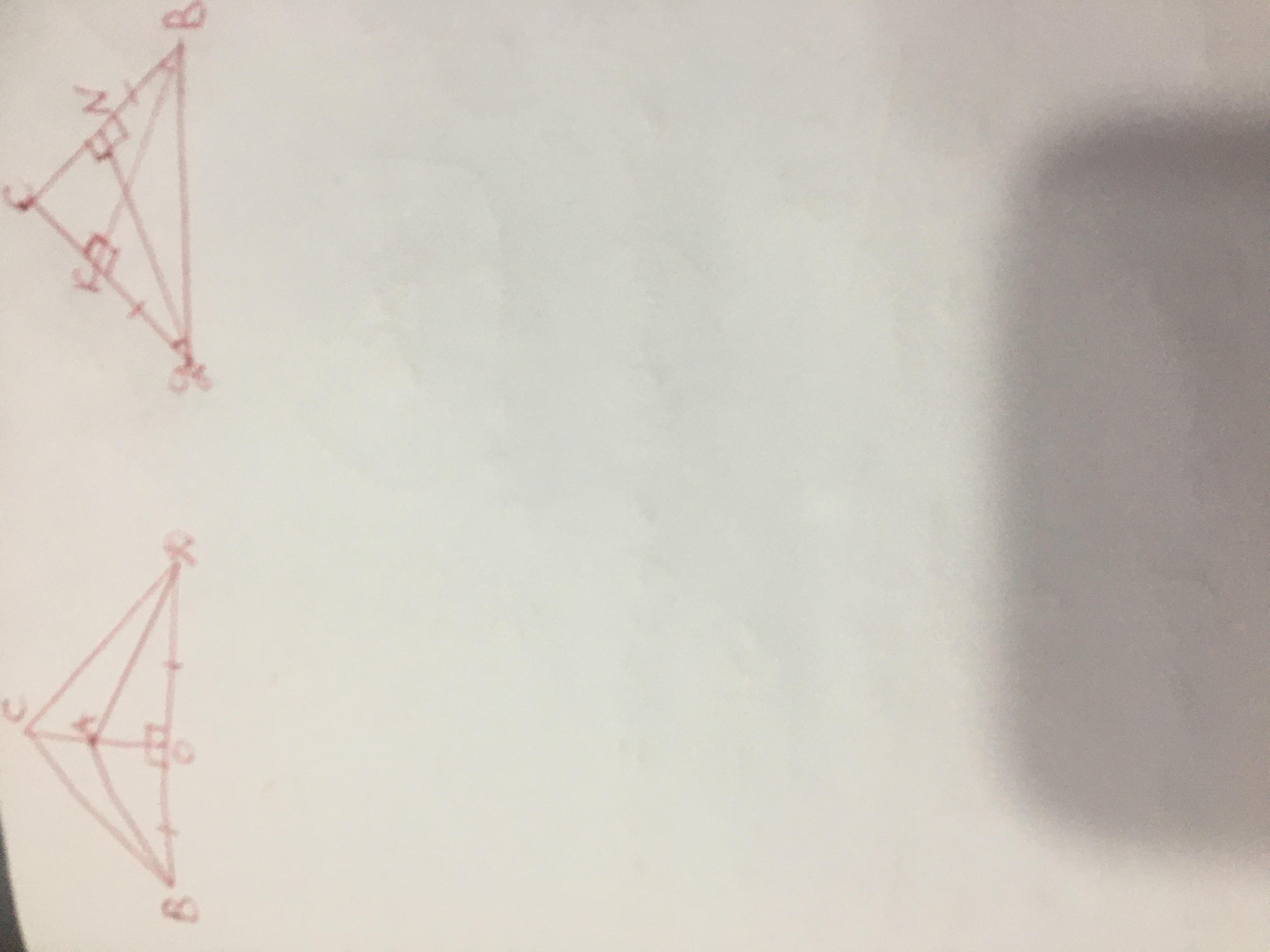
Помогите пожалуйста. (3 и 4)
Ответы
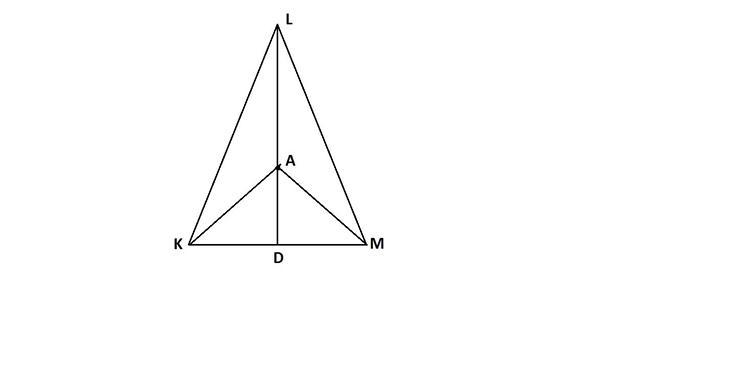
Проведём отрезки AK и AM.
Рассмотрим ΔKAD и ΔMAD.
∠KDA= ∠MDA = 90°, т.к. медиана в равнобедренном треугольнике, проведённая к основанию, является высотой.
KD = DM - т.к. LD - медиана
AD - общий катет
Значит, ΔKAD = ΔMAD - по двум катетам.
Из равенства треугольников ⇒ KA = AM ⇒ точка A равноудалена от вершин основания.
Ответ:
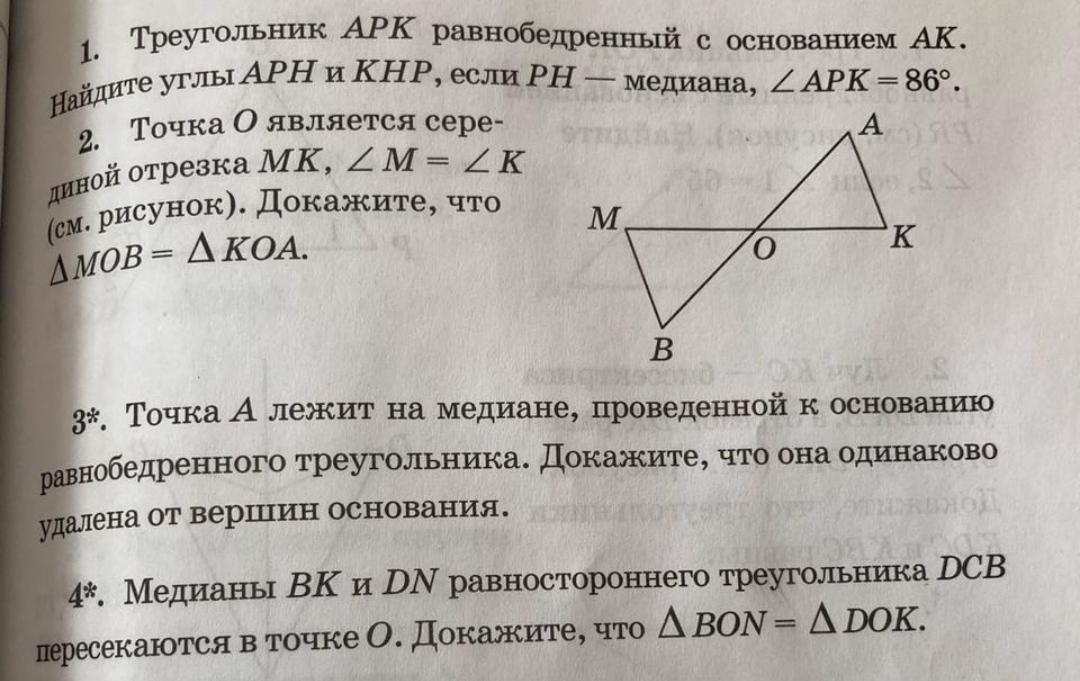
Номер 3
Точку А соединим с вершинами при основании и получилось 2 треугольника АВО и АОD
Так как СО медиана равнобедренного треугольника,то она поделила основание ВD на две равные части,значит
ВО=ОD
Так как треугольник равнобедренный,то медиана является и высотой,а это перпендикуляр на основание ВD,поэтому
<АОВ=<АОD=90 градусов
АО-общая сторона
По первому признаку равенства треугольников,по двум сторонам и углу между ними,треугольники АВО и АОD равны между собой,а следовательно
ВА=АD,что и требовалось доказать
Номер 4
Рассмотрим треугольники КОD и NOB
Так как КВ и DN медианы,то они поделили стороны CD и СВ на две равные части,значит
КD=NB
Так как треугольник равносторонний,то медиана одновременно является и высотой,т е перпендикуляром на СD и СВ,поэтому
<ОNB=<DKO=90 градусов
А так же медиана является и биссектрисой,поделила углы D и В на два равных угла,
<КDO=<NBO
По второму признаку равенства треугольников,по стороне и двум прилежащим к ней углам,треугольники равны
Объяснение: