Предмет: Математика,
автор: danyaisaevitch153
обчисліть площу фігури обмеженої лініями
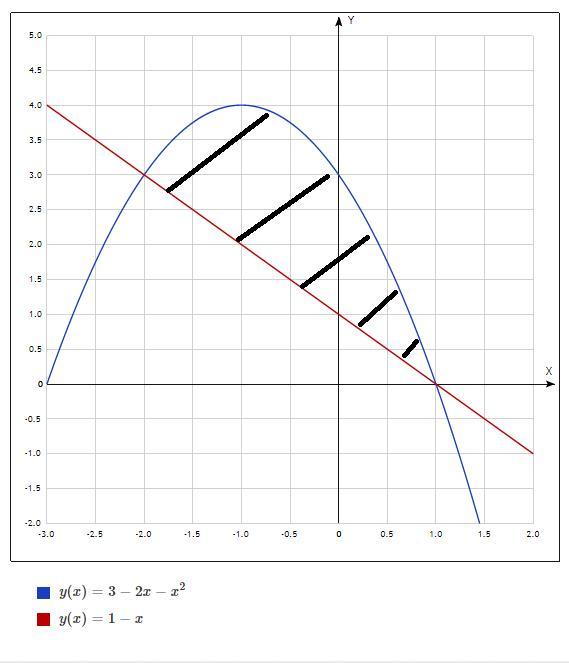
1)y=3-2x-x^2
і
2)x+y=1
Ответы
Автор ответа:
1
Приложения:
danyaisaevitch153:
а второе?
Похожие вопросы
Предмет: Русский язык,
автор: melissiya
Предмет: Английский язык,
автор: UnitedStates2015
Предмет: Французский язык,
автор: kachur001
Предмет: Алгебра,
автор: Аноним
Предмет: Окружающий мир,
автор: Аноним